Graficando ecuaciones cuadráticas usando la factorización
Una ecuación cuadrática es una ecuación polinomial de grado 2. La forma estándar de una ecuación cuadrática es
0 = ax 2 + bx + c
donde a, b, y c son todos los números reales y a ≠ 0.
Si reemplazamos 0 con y , entonces obtenemos una función cuadrática
y = ax 2 + bx + c
cuya gráfica será una parábola .
Los puntos donde la gráfica intersecta el eje de las x serán las soluciones a la ecuación, ax 2 + bx + c = 0. Esto es, si el polinomio ax 2 + bx + c puede factorizarse como ( x – p )( x – q ), sabemos por la propiedad del producto cero que si ( x – p )( x – q ) = 0, ya sea que ( x – p ) = 0 o ( x – q ) = 0. Entonces p y q son las soluciones a la ecuación ax 2 + bx + c = 0 y por lo tanto las intercepciones en x de la ecuación cuadrática.
Ya que la coordenada en
x
del
vértice de una parábola
es exactamente el punto medio de las
intercepciones en
x
, la coordenada en
x
del vértice será
.
Puede usar la coordenada en x del vértice para encontrar la coordenada en y .
Ahora Usted tiene el vértice y otros 2 puntos en la parábola (llamémoslos, las intercepciones en x ). Puede usar estos tres puntos para dibujar la gráfica.Ejemplo 1:
Grafique la función
usando la factorización.
Compare la ecuación con la forma estándar, y = ax 2 + bx + c . Ya que el valor de a es positivo, la parábola abre hacia arriba.
Factorice el trinomio,
.
Identifique 2 números cuya suma es –8 y el producto es 12. Los números son –2 y –6. Esto es,
.
Así, por la propiedad del producto cero, ya sea que x - 2 = 0 o x - 6 = 0. Entonces las raíces de la ecuación son 2 y 6.
Por lo tanto, las intercepciones en x de la función son 6 y 2.
La coordenada en
x
del vértice es el punto medio de las intercepciones en
x
. Así, aquí la coordenada en
x
del vértice será
.
Sustituya
x
= 4 en la ecuación
para encontrar la coordenada en
y
del vértice.
Esto es, las coordenadas del vértice son (4, –4).
Ahora tenemos 3 puntos (4, –4), (2,0) y (6,0) que están en la parábola. Grafique los puntos. Únalos por una curva suave y extienda la parábola.
Ejemplo 2:
Grafique la función
usando la factorización.
Compare la ecuación con la forma estándar, y = ax 2 + bx + c . Ya que el valor de a es positivo, la parábola abre hacia arriba.
Factorice el trinomio,
.
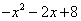Primero, factorice –1.
Factorice la expresión dentro del paréntesis. Identifique 2 números cuya suma es 2 y el producto es –8. Los números son 4 y -2. Esto es,
.
Entonces, la función dada se convierte en
.
Así, y = 0 implica, por la propiedad del producto cero, x + 4 = 0 o x - 2 = 0.
Por lo tanto, las intercepciones en x de la gráfica son –4 y 2.
La coordenada en
x
del vértice de una parabola es el punto medio de las intercepciones en
x
. Así, aquí la coordenada en
x
del vértice será
.
Sustituya
x
= -1 en la ecuación
para encontrar la coordenada en
y
del vértice.
Así, las coordenadas del vértice son (–1, 9).
Ahora tenemos 3 puntos (–1, 9), (–4, 0) y (2, 0) que están en la parábola. Grafique los puntos. Únalos por una curva suave y extienda la parábola.
