Factorización avanzada
Siempre puede usar la fórmula cuadrática para encontrar dos raíces de un trinomio cuadrático.
Pero a menudo, puede encontrar las raíces de forma más simple al factorizar.
Algunas veces, puede incluso usar la factorización para encontrar las raíces de una ecuación de orden superior, como un polinomio cúbico o de cuarto grado. A continuación, mostramos algunos casos especiales y como factorizarlos.Ejemplo 1:
Factorice el trinomio
.
Aquí, x es común en todos los términos y por lo tanto puede ser factorizada.
Necesitamos encontrar los dos números cuya suma es 7 y cuyo producto es 10 para factorizar
.
Los números son 2 y 5.
Por lo tanto,
.
Ejemplo 2:
Factorice el trinomio
.
Aquí,
es común en todos los términos y por lo tanto puede ser factorizada.
Necesitamos encontrar los dos números cuya suma es
y cuyo producto es
para factorizar
.
Entre las parejas de factores de
,
los dos números que tienen una suma de
son
y 2.
Así,
.
Por lo tanto,
.
Ejemplo 3:
Factorice,
.
Aquí, Usted tiene un polinomio de cuarto orden. Sustituya
para obtener un polinomio cuadrático equivalente
.
Necesitamos encontrar dos números cuya suma es 1 y cuyo producto es
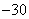para factorizar
.
Entre las parejas de factores de
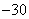, los dos números que tienen una suma de 1 son
y 6.
Así,
.
Esto es,
.
Puede usar la identidad
para reducir
como
.
El binomio
no se puede reducir; no puede factorizarse entre los números reales.
Por lo tanto,
.
Ejemplo 4:
Factorice el polinomio
.
Aquí, ninguno de los métodos anteriores servirá!
Agrupe los primeros 2 términos y los últimos 2 términos juntos.
Aquí,
es común en los primeros 2 términos y 4 es común en los 2 últimos términos. Factoricelos!
Ahora, factorice
.
El binomio
no se puede reducir; no puede factorizarse entre los números reales.
Por lo tanto,
.
Ejemplo 5:
Factorice el polinomio
.
Necesitamos encontrar dos números cuyo producto es igual al producto de los coeficientes de los términos
- y
- y cuya suma es igual al coeficiente del término medio. Esto es, dos números cuya suma es 7 y cuyo producto es 6 por 2 o 12.
Entre las parejas de factores de 12, los dos números que tienen una suma de 7 son 4 y 3.
Reescriba el término medio del trinomio usando los números.
Ahora, tenemos algo similar al polinomio del ejemplo 4. Así, agrupe los primeros 2 términos y los 2 últimos términos juntos.
Aquí,
es común en los primeros 2 términos y
y
es común en los 2 últimos términos. Factoricelos!
Ahora, use la propiedad distributiva .
Por lo tanto,
.
Vea también factorizando por grupos y polinomios no reducibles .
- Stochastic Modeling Tutors
- NNAT Courses & Classes
- Actuarial Exam SRM Test Prep
- Actuarial Exam IFM Test Prep
- UK GCSE Religious Studies Tutors
- ACCUPLACER Test Prep
- ACT Writing Courses & Classes
- CLEP German Tutors
- PCAT Biology Tutors
- Asian Studies Tutors
- CDR Exam - Cardiovascular Disease Recertification Exam Test Prep
- CLEP Calculus Tutors
- CFP Test Prep
- UK A Level Philosophy Tutors
- AU-M - Associate in Commercial Underwriting-Management Test Prep
- ISEE-Upper Level Writing Tutors
- Cognitive Psychology Tutors
- Social Statistics Tutors
- Series 28 Tutors
- Delaware Bar Exam Test Prep
