Área de superficie de una esfera
El matemático griego Arquímedes descubrió que el área de superficie de una esfera es igual al área lateral de superficie de un cilindro que tiene el mismo radio como la esfera y una altura de longitud del diámetro de la esfera.
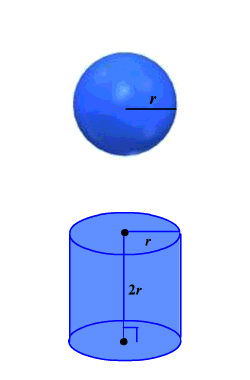
El área lateral de superficie del cilindro es 2 πrh donde h = 2 r .
Área lateral de superficie del cilindro = 2 πr (2 r ) = 4 π r 2 .
Por lo tanto, el área de superficie de una esfera con radio r es igual a 4 π r 2 .
Ejemplo :
Encuentre el área de superficie de una esfera con radio de 5 pulgadas.
S. A. = 4 π (5) 2 = 100 π pulgadas 2 ≈ 314.16 pulgadas 2
- Turkish Tutors
- AWS Certified SysOps Administrator Courses & Classes
- 10th Grade Math Tutors
- Series 26 Courses & Classes
- Real Estate License Test Prep
- Kansas Bar Exam Courses & Classes
- Series 24 Test Prep
- Series 26 Courses & Classes
- German Courses & Classes
- CPPA - Certified Professional Public Adjuster Courses & Classes
- AP Studio Art: Drawing Tutors
- GRE Subject Test in Chemistry Test Prep
- CCNA Industrial - Cisco Certified Network Associate-Industrial Test Prep
- AWS Certified SysOps Administrator Courses & Classes
- Gateway Test Tutors
- Series 57 Test Prep
- MAP Courses & Classes
- Alabama Bar Exam Test Prep
- Alaska Bar Exam Courses & Classes
- CLEP Test Prep