Resolviendo sistemas de ecuaciones lineales
Un sistema de ecuaciones lineales es solo un conjunto de dos o más ecuaciones lineales.
En dos variables ( x y y ), la gráfica de un sistema de dos ecuaciones es un par de rectas en el plano.
Hay tres posibilidades:
- Las rectas nunca se intersectan. (Las rectas son paralelas.)
- Las rectas se intersectan exactamente en un punto. (La mayoría de los casos.)
- Las rectas se intersectan infinitamente en muchos puntos. (Las dos ecuaciones representan la misma recta.)
Soluciones cero:
y = – 2 x + 4
y = –2 x – 3
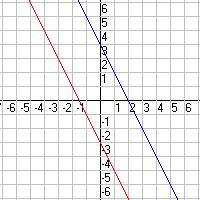
Una solución:
y = 0.5 x + 2
y = –2 x – 3
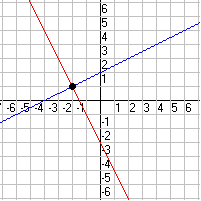
Infinitamente muchas soluciones:
y = –2 x – 4
y + 4 = –2 x
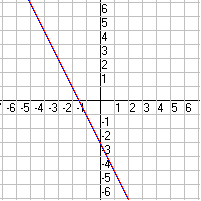
Hay unos pocos métodos diferentes de resolver sistemas de ecuaciones lineales:
- El método gráfico. Este es útil cuando solo necesita una respuesta aproximada, o está bastante seguro que la intersección ocurre en coordenadas enteras. Solo grafique las dos rectas, y vea donde se intersectan!
- El método de sustitución. Primero, resuelva una ecuación lineal para y en términos de x . Luego sustituya esa expresión por y en la otra ecuación lineal. Obtendrá una ecuación en x . Resuelva esta, y tendrá la coordenada en x de la intersección. Luego sustituya x en cualquier ecuación para encontrar la coordenada en y correspondiente. (Si es más fácil, puede iniciar resolviendo una ecuación para x en términos de y , también – misma diferencia!)
- El método de combinación lineal , también llamado el método de adición , también llamado el método de eliminación. Sume (o reste) un múltiplo de una ecuación a (o de) otra ecuación, de tal forma que ya sea los términos de x o los términos de y se eliminen. Luego resuelva para x (o y , la variable que se haya dejado) y sustituya para obtener la otra coordenada.
- El métdo de matrices . Este realmente solo es el método de combinación lineal, hecho más sencillo por la notación abreviada.
Vea la segunda gráfica anterior. La solución es donde las dos rectas se intersectan, el punto (–2, 1).
Ejemplo:
Resuelva el sistema
Resuelva la segunda ecuación para y .
y = 19 – 7 x
Sustituya 19 – 7 x por y en la primera ecuación y resuelva para x .
3 x + 2(19 – 7 x ) = 16
3 x + 38 – 14 x = 16
–11 x = –22
x = 2
Sustituya 2 por x en y = 19 – 7 x y resuelva para y .
y = 19 – 7(2)
y = 5
La solución es (2, 5).
Ejemplo:
Resuelva el sistema
Multiplique la primera ecuación por –2 y sume el resultado a la segunda ecuación.
–8 x – 6 y = 4
8 x – 2 y = 12
–8 y = 16
Resuelva para y .
y = –2
Sustituya por y en cualquiera de las ecuaciones originales y resuelva para x .
4 x + 3(–2) = –2
4 x – 6 = –2
4 x = 4
x = 1
La solución es (1, –2).
