We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Geometry

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #31 : Solid Geometry

The lateral area is twice as big as the base area of a cone. If the height of the cone is 9, what is the entire surface area (base area plus lateral area)?

Possible Answers:

90π

9π

54π

27π

81π

Correct answer:

81π

Explanation:

Lateral Area = LA = π(r)(l) where r = radius of the base and l = slant height

LA = 2B

π(r)(l) = 2π(r²)

rl = 2r²

l = 2r

Cone

From the diagram, we can see that r² + h² = l². Since h = 9 and l = 2r, some substitution yields

r² + 9² = (2r)²

r² + 81 = 4r²

81 = 3r²

27 = r²

B = π(r²) = 27π

LA = 2B = 2(27π) = 54π

SA = B + LA = 81π

Report an Error

Example Question #1 : How To Find The Surface Area Of A Cone

What is the surface area of a cone with a height of 8 and a base with a radius of 5?

Possible Answers:

$62.72\pi$

$25\pi$

$48.45\pi$

$65\pi$

Correct answer:

$62.72\pi$

Explanation:

To find the surface area of a cone we must plug in the appropriate numbers into the equation

$Surface\ Area=\pi r^{2}+\pi rl$

where is the radius of the base, and is the lateral, or slant height of the cone.

First we must find the area of the circle.

To find the area of the circle we plug in our radius into the equation of a circle which is

This yields $A=25\pi$ .

We then need to know the surface area of the cone shape.

To find this we must use our height and our radius to make a right triangle in order to find the lateral height using Pythagorean’s Theorem.

Pythagorean’s Theorem states

Take the radius and height and plug them into the equation as a and b to yield $5^{2}+8^{2}=c^{2}$

First square the numbers $25+64=c^{2}$

After squaring the numbers add them together $89=c^{2}$

Once you have the sum, square root both sides $\sqrt{89}=\sqrt{c^{2}}$

After calculating we find our length is c=l=9.43

Then plug the length into the second portion of our surface area equation above to get $(4)(\pi)(9.43)=37.72\pi$

Then add the area of the circle with the conical area to find the surface area of the entire figure $25\pi+37.72\pi=62.72\pi$

The answer is $62.72\pi$ .

Report an Error

Example Question #12 : Advanced Geometry

What is the surface area of a cone with a radius of 6 in and a height of 8 in?

Possible Answers:

112π in²

66π in²

60π in²

96π in²

36π in²

Correct answer:

96π in²

Explanation:

Find the slant height of the cone using the Pythagorean theorem: r² + h² = s² resulting in 6² + 8² = s² leading to s² = 100 or s = 10 in

SA = πrs + πr² = π(6)(10) + π(6)² = 60π + 36π = 96π in²

60π in² is the area of the cone without the base.

36π in² is the area of the base only.

Report an Error

Example Question #3 : How To Find The Surface Area Of A Cone

Find the surface area of a cone that has a radius of 12 and a slant height of 15.

Possible Answers:

$180\pi$

$324\pi$

$405\pi$

$144\pi$

$225\pi$

Correct answer:

$324\pi$

Explanation:

The standard equation to find the surface area of a cone is

$SA=\pi rs+\pi r^2$

where denotes the slant height of the cone, and denotes the radius.

Plug in the given values for and to find the answer:

$SA=\pi (12)(15)+\pi (12)^2=180\pi +144\pi =324\pi$

Report an Error

Example Question #4 : How To Find The Surface Area Of A Cone

Find the surface area of the following cone.

Cone

Possible Answers:

$100 \pi m^2$

$85 \pi m^2$

$90 \pi m^2$

$95 \pi m^2$

$80 \pi m^2$

Correct answer:

$90 \pi m^2$

Explanation:

The formula for the surface area of a cone is:

$SA = A_{base} + A_{lateral}$

$SA = \pi r^2 + \pi r l$

where is the radius of the cone and is the slant height of the cone.

Plugging in our values, we get:

$SA = \pi (5m)^2 + \pi (5m) (13m)$

$SA = 25 \pi m^2 + 65 \pi m^2 = 90 \pi m^2$

Report an Error

Example Question #5 : How To Find The Surface Area Of A Cone

Find the surface area of the following cone.

Cone

Possible Answers:

$116 \pi m^2$

$86 \pi m^2$

$96 \pi m^2$

$106 \pi m^2$

$76 \pi m^2$

Correct answer:

$96 \pi m^2$

Explanation:

The formula for the surface area of a cone is:

$SA = (base) + \frac{(circumference)(slant height)}{2}$

$SA = (\pi r^2) + \frac{(2 \pi r)(h_s)}{2}$

$SA = (\pi r^2) + ( \pi rh_s)$

Use the Pythagorean Theorem to find the length of the radius:

A^2 + B^2 = C^2

A^2 + (8m)^2 = (10m)^2

A = 6m

Plugging in our values, we get:

$SA = \pi (6m)^2 + \pi (6m)(10m)$

$SA = 96 \pi m^2$

Report an Error

Example Question #1 : How To Find The Surface Area Of A Cone

Find the surface area of the following half cone.

Half_cone

Possible Answers:

$120 \pi m^2 + 120 m^2$

$88 \pi m^2$

$88 \pi m^2 + 88 m^2$

$120 \pi m^2$

$100 \pi m^2 + 120 m^2$

Correct answer:

$100 \pi m^2 + 120 m^2$

Explanation:

The formula for the surface area of the half cone is:

$SA=(base)+\frac{1}{2}(circumference)(slant\ height)+(triangle)$

$SA=\left(\frac{\pi r^2}{2}\right)+\left(\frac{1}{2}\cdot \frac{2\pi r h_s}{2}\right)+rh$

Where is the radius, h_s is the slant height, and is the height of the cone.

Use the Pythagorean Theorem to find the height of the cone:

A^2+B^2 = C^2

A^2+(8m)^2=(17m)^2

A=15m

Plugging in our values, we get:

$SA=\left(\frac{\pi (8m)^2}{2}\right)+\left( \frac{\pi (8m) (17m)}{2}\right)+(8m)(15m)$

$SA=32 \pi m^2 + 68 \pi m^2 + 120m^2$

$SA = 100 \pi m^2 + 120 m^2$

Report an Error

Example Question #1 : How To Find The Surface Area Of A Polyhedron

Find the surface area of the following half-cylinder.

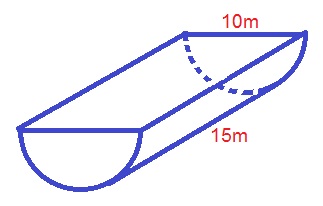
Half_cylinder

Possible Answers:

$150+100 \pi m^2$

$75\pi m^2$

$110 \pi m^2$

$90 \pi m^2$

$50+125 \pi m^2$

Correct answer:

$150+100 \pi m^2$

Explanation:

The formula for the surface area of a half-cylinder must include one-half of the surface area of a cylinder, which would be:

$SA = \frac{1}{2} (lateral\ area + 2 \cdot (base))$

We also need to add the area of the new rectangular face that is created by cutting the cylinder in half. The area of this rectangle would be:

$A=l\times w$

where the length of the rectangle is the same as the height of the half-cylinder, and the width of the rectangle is the same as the diameter of the base of the half-cylinder. So we can rewrite the area of the rectangle as:

$A=h\p\times d$

Now we can combine the two area formulas to find the total surface area of the half-cylinder:

$SA = \frac{1}{2} (2 \pi r (h) + 2 (\pi r^2))+h\cdot d$

$SA = \pi r (h) + \pi r^2+hd$

where is the radius of the base and is the length of the height, and is the diameter of the base.

Plugging in our values, we get:

$SA = \pi (5m) (15m) + \pi (5m)^2+15\cdot 10$

$SA = 75 \pi m^2 + 25 \pi m^2+150 = 150+100 \pi m^2$

Report an Error

Example Question #1 : How To Find The Surface Area Of A Polyhedron

Find the surface area of the following polyhedron.

Ice_cream_cone

Possible Answers:

$98 \pi m^2$

$108 \pi m^2$

$118 \pi m^2$

$88 \pi m^2$

$128 \pi m^2$

Correct answer:

$108 \pi m^2$

Explanation:

The formula for the surface area of the polyhedron is:

$SA = SA_{cone}+\frac{1}{2}SA_{sphere}$

$SA = \pi r l+\frac{1}{2}(4 \pi r^2)$

$SA = \pi r l+2 \pi r^2$

Where is the radius of the cone, is the slant height of the cone, and is the radius of the sphere

Use the formula for a 30-60-90 triangle to find the radius and slant height:

$a-a\sqrt{2}-2a$

$3\sqrt{3}m-9m-6\sqrt{3}m$

Plugging in our values, we get:

$SA = \pi r l+2 \pi r^2$

$SA = (\pi)(3\sqrt{3}m)(6\sqrt{3}m)+2(\pi)(3\sqrt{3}m)^2$

$SA = 54 \pi m^2 + 54 \pi m^2 = 108 \pi m^2$

Report an Error

Example Question #1 : Other Polyhedrons

Find the surface area of the following polyhedron.

Dome

Possible Answers:

$101 \pi m^2$

$71 \pi m^2$

$61 \pi m^2$

$91 \pi m^2$

$81 \pi m^2$

Correct answer:

$81 \pi m^2$

Explanation:

The formula for the surface area of the polyhedron is:

$SA = (cone:no\ base)+(cylinder:one\ base)$

$SA = \frac{1}{2}(circumference)(slant\ height)+(base)+(circumference)(height)$

$SA = \frac{1}{2}(2 \pi r)(h_s)+(\pi r^2)+(2 \pi r)(h)$

where is the radius of the cone, h_s is the slant height of the cone, is the radius of the cylinder, and is the height of the cylinder.

Use the formula for a 30-60-90 triangle to find the length of the radius:

$a-a\sqrt{3}-2a$

$3m-3\sqrt{3}m-6m$

Plugging in our values, we get:

$SA = \frac{1}{2}(2\pi (3m))(6m)+(\pi)(3m)^2+(2\pi (3m)(9m))$

$SA = 81 \pi m^2$

Report an Error

View Tutors

Benjamin
Certified Tutor

Portland State University, Bachelor of Science, Computer Science.

View Tutors

Robert
Certified Tutor

Rensselaer Polytechnic Institute, Bachelors, Electrical Engineering. Brooklyn Polytechnic, Masters, Computer Science.

View Tutors

Sanae
Certified Tutor

Case Western Reserve University, Current Undergrad Student, Japanese Studies.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Calculus Tutors in Boston, Chemistry Tutors in New York City, SAT Tutors in Washington DC, French Tutors in Los Angeles, SAT Tutors in Los Angeles, Physics Tutors in Boston, Chemistry Tutors in Boston, GRE Tutors in Atlanta, Reading Tutors in Miami, Calculus Tutors in New York City

Popular Courses & Classes

SSAT Courses & Classes in Houston, SSAT Courses & Classes in New York City, GMAT Courses & Classes in Los Angeles, GMAT Courses & Classes in Phoenix, SSAT Courses & Classes in Los Angeles, SAT Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in San Diego, MCAT Courses & Classes in Chicago, Spanish Courses & Classes in San Francisco-Bay Area, MCAT Courses & Classes in Philadelphia

Popular Test Prep

SAT Test Prep in Boston, MCAT Test Prep in Miami, MCAT Test Prep in Chicago, SAT Test Prep in Washington DC, LSAT Test Prep in New York City, GRE Test Prep in Boston, MCAT Test Prep in Seattle, GRE Test Prep in Los Angeles, SSAT Test Prep in Seattle, GMAT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Geometry

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #31 : Solid Geometry

Example Question #1 : How To Find The Surface Area Of A Cone

Example Question #12 : Advanced Geometry

Example Question #3 : How To Find The Surface Area Of A Cone

Example Question #4 : How To Find The Surface Area Of A Cone

Example Question #5 : How To Find The Surface Area Of A Cone

Example Question #1 : How To Find The Surface Area Of A Cone

Example Question #1 : How To Find The Surface Area Of A Polyhedron

Example Question #1 : How To Find The Surface Area Of A Polyhedron

Example Question #1 : Other Polyhedrons

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: