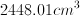We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Geometry

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : How To Find The Volume Of A Cube

What is the volume of a cube with a side length of 7?

Possible Answers:

300

343

Correct answer:

343

Explanation:

When searching for the volume of a cube we are looking for the amount of the space enclosed by the cube.

To find this we must know the formula for the volume of a cube which is $Volume\: of\: Cube=s^{3}$

Using this formula we plug in the side length for to get $V=7^{3}$

Cube the side length to arrive at the answer of $7^{3}=343$

The answer is 343 .

Report an Error

Example Question #3 : How To Find The Volume Of A Cube

If the volume of a cube is 3375, what is the length of each side?

Possible Answers:

843.75

Correct answer:

Explanation:

To find this we must know the formula for the volume of a cube which is

We plug the volume into the equation yielding $3375= s^{3}$

Then we take the cube root of both sides giving us $\sqrt[3]{3375}=\sqrt[3]{s^{3}}$

We now know 15=s

The answer is .

Report an Error

Example Question #1 : How To Find The Volume Of A Cube

What is the sum of the number of vertices, edges, and faces of a cube?

Possible Answers:

None of the answers are correct

Correct answer:

Explanation:

Vertices = three planes coming together at a point = 8

Edges = two planes coming together to form a line = 12

Faces = one plane as the surface of the solid = 6

Vertices + Edges + Faces = 8 + 12 + 6 = 26

Report an Error

Example Question #4 : How To Find The Volume Of A Cube

What is the volume, in centimeters, of a rectangular prism with a length of l=2.4cm , a width of w=255mm , and a height of h=0.44m ?

Possible Answers:

$2692.8cm^{3}$

$2448.01cm^{3}$

$\dpi{100}269.28 cm^{3}$

$26928cm^{3}$

$\dpi{100} 2962.8cm^{3}$

Correct answer:

$2692.8cm^{3}$

Explanation:

In order to solve this problem, we need to make sure that the measurements given are in uniform units. In this case, we will use centimeters; therefore, we need to convert the other units of meters and millimeters into centimeters via dimensional analysis.

Solve for the width.

$w=\frac{255mm}{1}*\frac{1cm}{10mm}$

w=25.5cm

Solve for the height.

$h=\frac{0.44m}{1}*\frac{100cm}{1m}$

h=44cm

Now, solve for volume by using the formula V=l*w*h .

V=2.4cm*25.5cm*44cm

$\rightarrow 2692.8cm^{3}$

If you calculated $\dpi{100}269.28 cm^{3}$ , then you did not convert into appropriate units.

Report an Error

Example Question #5 : How To Find The Volume Of A Cube

Square_with_diagonal What is the volume of a cube with a diagonal one one of its faces of $\dpi{100} d=6.27ft$ ?

Possible Answers:

$78.51ft^{3}$

Not enough information to solve

$264.50ft^{3}$

$246.50ft^{3}$

$87.15ft^{3}$

Correct answer:

$87.15ft^{3}$

Explanation:

A few facts need to be known to solve this problem. Observe that the diagonal of the square face of the cube cuts the qradilateral into two right isosceles triangles; therefore, the length of a side of the square to its diagonal is the same as an isosceles right triangle's leg to its hypotenuse: $1:\sqrt{2}$ .

$\frac{s}{d}=\frac{1}{\sqrt{2}}$

$\dpi{100} \dpi{100} \dpi{100} \frac{s}{6.27ft}=\frac{1}{\sqrt{2}}$

Rearrange an solve for .

$\dpi{100} \dpi{100} s=\frac{6.27ft}{\sqrt{2}}$

Now, solve for the volume.

$V=s^{3}$

$V=(\frac{6.27ft}{\sqrt{2}})*(\frac{6.27ft}{\sqrt{2}})*(\frac{6.27ft}{\sqrt{2}})$

$V=\frac{246.491883ft^{3}}{2\sqrt{2}}$

$\rightarrow87.15ft^{3}$

Report an Error

Example Question #6 : How To Find The Volume Of A Cube

A building is in the shape of a perfect cube, with a side length of s=0.44miles . What is the building's volume, in cubic meters?

Possible Answers:

$535000000m^{3}$

Not enough information to solve

$500000000m^{3}$

$85184m^{3}$

$355000000m^{3}$

Correct answer:

$355000000m^{3}$

Explanation:

In order to solve this question, we need to convert miles to meters via dimensional analysis and then solve for the volume of the building.

$s=\frac{0.44 mi}{1}*\frac{1.60934km}{1mi}*\frac{1000m}{1km}$

s=708.1096m

Now, solve for volume.

$V=s^{3}$

$V=(708.1096m)^{3}$

$\rightarrow 355059753.12m^{3}\rightarrow 355000000m^{3}$

Report an Error

Example Question #1 : How To Find The Volume Of A Cube

This figure is a cube with one face having an area of 16 in². Cube

What is the volume of the cube (in³)?

Possible Answers:

128

4096

256

Correct answer:

Explanation:

The volume of a cube is one side cubed. Because we know that one face has an area of 16 in², then we know that one side must be the square root of 16 or 4. Thus the volume is $4^{3}=64$ .

Report an Error

Example Question #2 : How To Find The Volume Of A Cube

A cube has a height of 4 feet. What is the volume of the cube in feet?

Possible Answers:

128

256

Correct answer:

Explanation:

We only have the length of one edge, but that is sufficient for finding the volume. The volume of a cube equals one edge multiplied by itself three times: $e^{3}$

$4^{3}=64$

Report an Error

Example Question #8 : How To Find The Volume Of A Cube

A cube has a surface area of 294 units squared. What is its volume?

Possible Answers:

216 units cubed

729 units cubed

512 units cubed

343 units cubed

Correct answer:

343 units cubed

Explanation:

Since a cube has square faces and the surface area of each face is given by multiplying the length of one side of the square face by itself, the equation for the surface area of a cube is A = 6s^2 , where is the length of one side of one face (i.e., one edge of the cube). Find the length of one side/edge of the given cube by setting the given surface area equal to 6s^2 :

6s^2 = 294

$\rightarrow s^2 = 49$

$\rightarrow s = 7$ units

The volume of a cube is s^3 , where is the length of one of the cube's edges. Substituing the solution to the previous equation for in the volume equation gives the volume of the cube:

V = s^3

$\rightarrow V = (7)^3$

$\rightarrow V = 343$ units cubed

Report an Error

Example Question #591 : Geometry

Find the volume of the following cube:

Length_of_diagonal

Possible Answers:

$56\ m^3$

$60\ m^3$

$68\ m^3$

$52\ m^3$

$64\ m^3$

Correct answer:

$64\ m^3$

Explanation:

The formula for the volume of a cube is

V=(s)^3 ,

where is the side of the cube.

Plugging in our values, we get:

$V=(4\ m)^3$

$V=64\ m^3$

Report an Error

View Tutors

Grace
Certified Tutor

St John's University-New York, Bachelor in Arts, Psychology. University of Bridgeport, Masters in Education, Education.

View Tutors

Shiva Tej
Certified Tutor

Vellore Institute of Technology, Bachelor of Science, Mechanical Engineering. University of Toronto, Master of Science, Data ...

View Tutors

Paige
Certified Tutor

Geneva College, Bachelor in Arts, General Literature.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SSAT Tutors in Philadelphia, Spanish Tutors in Los Angeles, SAT Tutors in Atlanta, Physics Tutors in Los Angeles, Statistics Tutors in Houston, ISEE Tutors in Washington DC, ACT Tutors in Houston, GRE Tutors in Dallas Fort Worth, English Tutors in New York City, GMAT Tutors in Los Angeles

Popular Courses & Classes

ISEE Courses & Classes in Los Angeles, GMAT Courses & Classes in New York City, Spanish Courses & Classes in Washington DC, Spanish Courses & Classes in Dallas Fort Worth, ACT Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Washington DC, GMAT Courses & Classes in Denver, MCAT Courses & Classes in Phoenix, SAT Courses & Classes in San Diego, LSAT Courses & Classes in New York City

Popular Test Prep

ISEE Test Prep in San Diego, LSAT Test Prep in San Francisco-Bay Area, SAT Test Prep in Washington DC, LSAT Test Prep in Seattle, ACT Test Prep in Dallas Fort Worth, LSAT Test Prep in New York City, ISEE Test Prep in Denver, ACT Test Prep in San Diego, GRE Test Prep in Boston, GMAT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Geometry

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #2 : How To Find The Volume Of A Cube

Example Question #3 : How To Find The Volume Of A Cube

Example Question #1 : How To Find The Volume Of A Cube

Example Question #4 : How To Find The Volume Of A Cube

Example Question #5 : How To Find The Volume Of A Cube

Example Question #6 : How To Find The Volume Of A Cube

Example Question #1 : How To Find The Volume Of A Cube

Example Question #2 : How To Find The Volume Of A Cube

Example Question #8 : How To Find The Volume Of A Cube

Example Question #591 : Geometry

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: