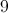We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Geometry

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #242 : New Sat Math Calculator

$\dpi{100} \small \overline{AB}$ is a straight line. $\dpi{100} \small \overline{CD}$ intersects $\dpi{100} \small \overline{AB}$ at point $\dpi{100} \small E$ . If $\dpi{100} \small \angle AEC$ measures 120 degrees, what must be the measure of $\dpi{100} \small \angle BEC$ ?

Possible Answers:

$\dpi{100} \small 75$ degrees

None of the other answers

$\dpi{100} \small 70$ degrees

$\dpi{100} \small 60$ degrees

$\dpi{100} \small 65$ degrees

Correct answer:

$\dpi{100} \small 60$ degrees

Explanation:

$\dpi{100} \small \angle AEC$ & $\dpi{100} \small \angle BEC$ must add up to 180 degrees. So, if $\dpi{100} \small \angle AEC$ is 120, $\dpi{100} \small \angle BEC$ (the supplementary angle) must equal 60, for a total of 180.

Report an Error

Example Question #11 : Geometry

If $\overleftrightarrow{FH} \parallel \overleftrightarrow{AD}$ , $\overline{BE}\perp \overleftrightarrow{GC}$ , and $m\angle HGC=58^\circ$ , what is the measure, in degrees, of $\angle ABE$ ?

Alternate interior angles

Possible Answers:

122

148

Correct answer:

148

Explanation:

The question states that $\overleftrightarrow{FH} \parallel \overleftrightarrow{AD}$ . The alternate interior angle theorem states that if two parallel lines are cut by a transversal, then pairs of alternate interior angles are congruent; therefore, we know the following measure:

$m\angle GCA = 58^\circ$

The sum of angles of a triangle is equal to 180 degrees. The question states that $\overline{BE}\perp \overleftrightarrow{GC}$ ; therefore we know the following measure:

$m \angle BEC = 90^\circ$

Use this information to solve for the missing angle: $\angle EBC$

$180^\circ=m\angle EBC+58^\circ+90^\circ$

$m\angle EBC=32^\circ$

The degree measure of a straight line is 180 degrees; therefore, we can write the following equation:

$180^\circ=m\angle ABE+32^\circ$

$m\angle ABE=148^\circ$

The measure of $\angle ABE$ is 148 degrees.

Report an Error

Example Question #1 : How To Find The Perimeter Of A Hexagon

What is the perimeter of a regular hexagon with a side length of 12?

Possible Answers:

Correct answer:

Explanation:

To find the perimeter of a regular hexagon you must first know the number of sides in a hexagon which is 6.

When you know the number of sides of a regular polygon to find the perimeter you must multiply the side length by the number of sides.

In this case it is 6*12=72

The answer for the perimeter is .

Report an Error

Example Question #1 : Hexagons

How many degrees is the interior angle of any regular hexagon?

Possible Answers:

120^o

160^o

90^o

60^o

Correct answer:

120^o

Explanation:

$interior\ angle=\frac{(n-2)*180^o}{n}$

To find the angle of any regular polygon, you find the number of sides, . In this example n=6 .

$interior\ angle=\frac{(n-2)*180^o}{n}=\frac{(6-2)*180^o}{6}$

You then subtract from the number of sides, yielding .

Take and multiply it by 180^o to yield the total number of degrees in the regular hexagon.

(n-2)*180^o=4*180^o=720^o

Then, to find one individual angle, we divide 720^o by the total number of angles, .

$\frac{720^o}{6}=120^o$

The answer is 120^o .

Report an Error

Example Question #1 : How To Find The Perimeter Of A Hexagon

What is the perimeter of a hexagon with a side length of ?

Possible Answers:

Correct answer:

Explanation:

To find the perimeter of a regular polygon, we take the length of each side, , and multiply it by the number of sides, .

P=s*l

In a hexagon the number of sides is , and in this example the side length is .

P=6*4=24

The perimeter is .

Report an Error

Example Question #1 : How To Find The Perimeter Of A Hexagon

How many lines of symmetry can be found in a regular hexagon?

Possible Answers:

$\infty$

Correct answer:

Explanation:

The number of lines of symmetry through a regular polygon is equal to the number of sides.

A hexagon has lines of symmetry through each vertex, giving three lines of symmetry that each connect two opposite vertices. The other three lines pass through the midpoints of opposite sides of the hexagon.

Report an Error

Example Question #2 : How To Find The Perimeter Of A Hexagon

What is the perimeter of a regular hexagon with a side length of ?

Possible Answers:

Correct answer:

Explanation:

To find the perimeter of a regular hexagon you must first know the number of sides in a hexagon which is .

When you know the number of sides of a regular polygon to find the perimeter you must multiply the side length by the number of sides.

In this case it is 6*12=72

The answer for the perimeter is .

Report an Error

Example Question #1 : How To Find The Perimeter Of A Hexagon

This figure is a regular hexagon with one side measuring 6 cm. Hexagon

What is the perimeter of the regular hexagon in centimeters?

Possible Answers:

Correct answer:

Explanation:

The perimeter of a regular hexagon is just the sum of all 6 sides. Because it's a regular hexagon, the perimemter is just six times one side (6 cm) or 36 cm.

Report an Error

Example Question #1 : How To Find The Length Of The Diagonal Of A Hexagon

What is the length of a diagonal of a regular hexagon with side length ?

Possible Answers:

5.7

11.4

Correct answer:

Explanation:

Regular hexagons are comprised of six equilateral triangles; in our question, these triangles each have side length 4 (see diagram).

Hectagon

The length of a diagonal is equal to two times the length of the side. In this instance, the answer is 8.

2*4=8

Report an Error

Example Question #1 : How To Find The Length Of The Diagonal Of A Hexagon

How many diagonals are there in a regular hexagon?

Possible Answers:

Correct answer:

Explanation:

A diagonal is a line segment joining two non-adjacent vertices of a polygon. A regular hexagon has six sides and six vertices. One vertex has three diagonals, so a hexagon would have three diagonals times six vertices, or 18 diagonals. Divide this number by 2 to account for duplicate diagonals between two vertices. The formula for the number of vertices in a polygon is:

$\frac{n\cdot (n-3)}{2}$

where $n=\#\ of\ sides$ .

Report an Error

View Tutors

Beth Ann
Certified Tutor

Missouri State University-Springfield, Bachelor in Arts, English. William Woods University, Master of Arts, Elementary School...

View Tutors

Yoonsik
Certified Tutor

Seoul National University, Bachelor of Science, Physics. University of Pennsylvania, Doctor of Philosophy, Atomic and Molecul...

View Tutors

Melissa
Certified Tutor

West Virginia University Institute of Technology, Bachelor of Science, Human Services. Old Dominion University, Master of Sci...

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Physics Tutors in Houston, Physics Tutors in Dallas Fort Worth, GRE Tutors in Boston, Math Tutors in Miami, GMAT Tutors in Dallas Fort Worth, GRE Tutors in Washington DC, Calculus Tutors in Los Angeles, SSAT Tutors in Atlanta, Math Tutors in Washington DC, English Tutors in Boston

Popular Courses & Classes

GMAT Courses & Classes in San Diego, SAT Courses & Classes in Philadelphia, ISEE Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in Denver, ACT Courses & Classes in Phoenix, LSAT Courses & Classes in Houston, GMAT Courses & Classes in Denver, SSAT Courses & Classes in Washington DC, GMAT Courses & Classes in Houston, GMAT Courses & Classes in Atlanta

Popular Test Prep

GMAT Test Prep in Atlanta, GMAT Test Prep in Boston, GRE Test Prep in Houston, GRE Test Prep in Denver, SAT Test Prep in Dallas Fort Worth, MCAT Test Prep in Washington DC, LSAT Test Prep in Chicago, ACT Test Prep in Dallas Fort Worth, ISEE Test Prep in Boston, LSAT Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Geometry

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #242 : New Sat Math Calculator

Example Question #11 : Geometry

Example Question #1 : How To Find The Perimeter Of A Hexagon

Example Question #1 : Hexagons

Example Question #1 : How To Find The Perimeter Of A Hexagon

Example Question #1 : How To Find The Perimeter Of A Hexagon

Example Question #2 : How To Find The Perimeter Of A Hexagon

Example Question #1 : How To Find The Perimeter Of A Hexagon

Example Question #1 : How To Find The Length Of The Diagonal Of A Hexagon

Example Question #1 : How To Find The Length Of The Diagonal Of A Hexagon

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: