All High School Math Resources
Example Questions
Example Question #18 : Spheres
Find the surface area of a sphere whose diameter is 
The surface area of a sphere is found by the formula 

Now, we can solve for surface area.
Example Question #1 : How To Find The Surface Area Of A Sphere
To the nearest tenth of a square centimeter, give the surface area of a sphere with volume 1,000 cubic centimeters.
The volume of a sphere in terms of its radius 
Substitute 

Substitute for 
Example Question #1 : How To Find The Surface Area Of A Sphere
Find the surface area of a sphere with a radius of 
The standard equation to find the area of a sphere is 
Substitute the given radius into the standard equation to get the answer:
Example Question #1 : How To Find The Surface Area Of A Sphere
Given that the radius of a sphere is 3, find the surface area.
The standard equation to find the area of a sphere is
where 
Example Question #4 : How To Find The Surface Area Of A Sphere
Find the surface area of the following sphere.

The formula for the surface area of a sphere is:
where 
Plugging in our values, we get:
Example Question #5 : How To Find The Surface Area Of A Sphere
Find the surface area of the following sphere.

The formula for the surface area of a sphere is:
Where 
Plugging in our values, we get:
Example Question #2001 : High School Math
What is the surface area of a composite figure of a cone and a sphere, both with a radius of 5 cm, if the height of the cone is 12 cm? Consider an ice cream cone as an example of the composite figure, where half of the sphere is above the edge of the cone.
Calculate the slant height height of the cone using the Pythagorean Theorem. The height will be the height of the cone, the base will be the radius, and the hypotenuse will be the slant height.
The surface area of the cone (excluding the base) is given by the formula 
The surface area of a sphere is given by 

So the total surface area of the composite figure is 
Example Question #2002 : High School Math
What is the surface area of a hemisphere with a diameter of 
A hemisphere is half of a sphere. The surface area is broken into two parts: the spherical part and the circular base.
The surface area of a sphere is given by 
So the surface area of the spherical part of a hemisphere is 
The area of the circular base is given by 
Example Question #2003 : High School Math
What is the surface area of a sphere with a radius of 
To solve for the surface area of a sphere you must remember the formula:
First, plug the radius into the equation for 
Since 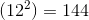

The answer is therefore 
Example Question #1 : How To Find The Diameter Of A Sphere
What is the diameter of a sphere with a volume of 
To find the diameter of a sphere we must use the equation for the volume of a sphere to find the radius which is half of the diameter.
The equation is
First we enter the volume into the equation yielding
We then divide each side by to get
We then multiply each side by to get
We then take the cubic root of each side to solve for the radius
The radius is
We then multiply the radius by 2 to find the diameter
The answer for the diameter is 
All High School Math Resources






















![r=\sqrt[3]{ \frac{3,000}{4\pi }} \approx 6.20 \textrm{ cm }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/100061/gif.latex)















































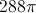


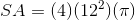
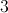






![\sqrt[3]{27}=\sqrt[3]{r^{3}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/135793/gif.latex)




