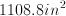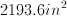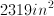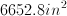The surface area of a cube can be determined using the following equation:

\(\displaystyle SA=6\times l^2\)

\(\displaystyle 54=6l^2\)

\(\displaystyle \frac{54}{6}=\frac{6l^2}{6}\)

\(\displaystyle 9=l^2\)

\(\displaystyle \sqrt9=\sqrt{l^2}\)

\(\displaystyle 3=l\)

Find the diagonal of one face of the cube using the Pythagorean Theorem applied to a triangle formed by two sides of that face (\(\displaystyle a\) and \(\displaystyle b\)) and the diagonal itself (\(\displaystyle c\)):

\(\displaystyle a^2 + b^2 = c^2\)

\(\displaystyle (2\sqrt{2})^2 + (2\sqrt{2})^2 = c^2\)

\(\displaystyle \rightarrow 8 + 8 = c^2\)

\(\displaystyle \rightarrow 16 = c^2\)

\(\displaystyle \rightarrow c = 4\)

This diagonal is now the base of a new right triangle (call this \(\displaystyle b\)). The height of that triangle is an edge of the cube that runs perpendicular to this diagonal (call this \(\displaystyle a\)). The third side of the triangle formed by \(\displaystyle a\) and \(\displaystyle b\) is a line from one corner of the cube to the other, i.e., the cube's diagonal (call this \(\displaystyle c\)). Use the Pythagorean Theorem again with the triangle formed by \(\displaystyle a\), \(\displaystyle b\), and \(\displaystyle c\) to find the length of this diagonal.

\(\displaystyle a^2 + b^2 = c^2\)

\(\displaystyle (2\sqrt{2})^2 + (4)^2 = c^2\)

\(\displaystyle \rightarrow 8 + 16 = c^2\)

\(\displaystyle \rightarrow 24 = c^2\)

\(\displaystyle \rightarrow \sqrt{24} = c\)

\(\displaystyle \rightarrow c= 2\sqrt{6}\)

To find the length of the diagonal, use the formula for a \(\displaystyle 45-45-90\) triangle:

\(\displaystyle a-a-a\sqrt{2}\)

\(\displaystyle 4\ m-4\ m-4\sqrt{2}\ m\)

The length of the diagonal is \(\displaystyle 4\sqrt{2}\ m\).

To find the surface area of a cube we must count the number of surface faces and add the areas of each of them together.

In a cube there are 6 faces, each a square with the same side lengths.

In this example the side lengths is 15 so the area of each square would be \(\displaystyle 15^2=225\)

We then multiply this number by 6, the number of faces of the cube, to get \(\displaystyle 225*6=1350\)

Our answer for the surface area is \(\displaystyle 1350\).

To find the surface area of a cube, we must count the number of surface faces and add the areas of each together. In a cube there are \(\displaystyle 6\) faces, each a square with the same side lengths. In this example the side length is \(\displaystyle 7\).

The area of a square is given by the equation \(\displaystyle A=s*s=s^2\). Using our side length, we can solve the area of once face of the cube.

\(\displaystyle A=(7)^{2}=49\)

We then multiply this number by \(\displaystyle 6\), the number of faces of the cube to find the total surface area.

\(\displaystyle 49*6=294\)

Our answer for the surface area is \(\displaystyle 294\).

The surface area of a cube = 6a² where a is the length of the side of each edge of the cube. Put another way, since all sides of a cube are equal, a is just the lenght of one side of a cube.

We have 96 = 6a² → a² = 16, so that's the area of one face of the cube.

Solving we get √16, so a = 4

In order to find the surface area of a cube, use the formula \(\displaystyle SA=6(s^{2})\).

\(\displaystyle SA=6*(7.2in)^{2}\)

\(\displaystyle SA=6*51.84in^{2}\)

\(\displaystyle SA=311.04in^{2}\)

\(\displaystyle \rightarrow 311in^{2}\)

In order to find the surface area of a rectangular prism, use the formula \(\displaystyle SA=(2*lw)+(2*wh)+(2*lh)\).

However, all units must be the same. All of the units of this problem are in inches with the exception of \(\displaystyle \dpi{100} l=2.2ft\).

Convert to inches.

\(\displaystyle l=\frac{2.2ft}{1}*\frac{12in}{1ft}\)

\(\displaystyle l=26.4in\)

Now, we can insert the known values into the surface area formula in order to calulate the surface area of the rectangular prism.

\(\displaystyle SA=(2*26.4in*18in)+(2*18in*14in)+(2*26.4in*14in)\)

\(\displaystyle SA=(950.4in^{2})+(504in^{2})+(739.2in^{2})\)

\(\displaystyle SA=2193.6in^{2}\)

If you calculated the surface area to equal \(\displaystyle 6652.8in^{2}\), then you utilized the volume formula of a rectangular prism, which is \(\displaystyle V=l*w*h\); this is incorrect.

A few facts need to be known to solve this problem. Observe that the diagonal of the square face of the cube cuts it into two right isosceles triangles; therefore, the length of a side of the square to its diagonal is the same as an isosceles right triangle's leg to its hypotenuse: \(\displaystyle 1:\sqrt{2}\).

\(\displaystyle \frac{s}{d}=\frac{1}{\sqrt{2}}\)

\(\displaystyle \dpi{100} \dpi{100} \frac{s}{4.2cm}=\frac{1}{\sqrt{2}}\)

Rearrange an solve for \(\displaystyle s\).

\(\displaystyle \dpi{100} s=\frac{4.2cm}{\sqrt{2}}\)

Now, solve for the area of the cube using the formula \(\displaystyle \dpi{100} \dpi{100} SA=6(s^{2})\).

\(\displaystyle SA=6*(\frac{4.2cm}{\sqrt{2}})^{2}\)

\(\displaystyle SA=\frac{6}{1}*(\frac{4.2cm}{\sqrt{2}}*\frac{4.2cm}{\sqrt{2}})\)

\(\displaystyle \dpi{100} SA=\frac{6}{1}*(\frac{17.64cm^{2}}{2})\)

\(\displaystyle \dpi{100} \dpi{100} SA=3*17.64cm^{2}\)

\(\displaystyle \rightarrow 52.92cm^{2}\)

The surface area of a cube is the sum of the area of each face.  Since there are 6 faces on a cube, the surface area of the entire cube is \(\displaystyle 6\cdot16\).