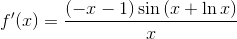Call Now to Set Up Tutoring:

(888) 888-0446

AP Calculus AB : Computation of the Derivative

Study concepts, example questions & explanations for AP Calculus AB

Create An Account

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #61 : Chain Rule And Implicit Differentiation

Find the derivative of the function

$w(x)=\sin(\tan{x})$

Possible Answers:

$w'(x)=\sec^2(x)-\cos(\tan{x})$

$w'(x)=\sec^2(x)\cos(\tan{x})$

$w'(x)=\sec^2(x)\sin(\tan{x})$

$w'(x)=\sec(x)\cos(\tan{x})$

Correct answer:

$w'(x)=\sec^2(x)\cos(\tan{x})$

Explanation:

To find the derivative of the function, you must apply the chain rule, which is as follows:

$\frac{\mathrm{d} }{\mathrm{d} x}(p(g(x)))=p'(g(x))(g'(x))$

Using the function from the problem statement, we have that

$g(x)=\tan(x)$ and $p(g(x))=\sin(\tan(x))$

Following the rule, we get

$w'(x)=\sec^2(x)\cos(\tan(x))$

Report an Error

Example Question #62 : Chain Rule And Implicit Differentiation

$f(x) = \cos (x+ \ln x)$

Find f'(x) .

Possible Answers:

None of the other choices gives the correct response.

$f'(x)= \frac{(x+1)\sin \left ( x + \ln x \right )}{x}$

$f'(x)= \frac{(-x- 1)\sin \left ( x + \ln x \right )}{x}$

$f'(x)= \frac{(-x- 1)\sin \left ( x - \ln x \right )}{x}$

$f'(x)= \frac{(x+1)\sin \left ( x - \ln x \right )}{x}$

Correct answer:

$f'(x)= \frac{(-x- 1)\sin \left ( x + \ln x \right )}{x}$

Explanation:

Let $u(x) = x + \ln x$

Then

$f(x) = \cos u$

and

$f'(x)= \frac{\mathrm{d} }{\mathrm{d} x} \cos (u(x))$

Apply the chain rule:

$f'(x)= \frac{\mathrm{d} u}{\mathrm{d} x} \cdot \frac{\mathrm{d} }{\mathrm{d} u} \cos u$

$f'(x)= \frac{\mathrm{d} }{\mathrm{d} x}( x + \ln x) \cdot( - \sin u)$

Substitute back for :

$f'(x)= \frac{\mathrm{d} }{\mathrm{d} x}( x + \ln x) \cdot( - \sin \left ( x + \ln x \right ))$

Apply the sum rule:

$f'(x)=\left ( \frac{\mathrm{d} }{\mathrm{d} x}( x ) + \frac{\mathrm{d} }{\mathrm{d} x}( \ln x) \right )\cdot( - \sin \left ( x + \ln x \right ))$

$f'(x)=\left ( 1 + \frac{1}{x} \right )\cdot( - \sin \left ( x + \ln x \right ))$

After some simple algebra:

$f'(x)=\left ( \frac{x+ 1}{x} \right )\cdot( - \sin \left ( x + \ln x \right ))$

$f'(x)= \frac{(-x- 1)\sin \left ( x + \ln x \right )}{x}$

Report an Error

Example Question #161 : Computation Of The Derivative

is a function of . Solve for in this differential equation:

$\frac{\mathrm{d} y}{\mathrm{d} x}= \frac{xy}{x^{2}+ 2}$

Possible Answers:

$y =\frac{C\sqrt{ x^{2}+ 2} }{ x^{2}+ 2}$

$y =C \sqrt{ x^{2}+ 2}$

$y =C e^{\sqrt{ \frac{1}{3}x^{3}+ 2x}}$

$y = \frac{1}{3}x^{3}+ 2x+ C$

$y =C e^{\sqrt{ x^{2}+ 2}}$

Correct answer:

$y =C \sqrt{ x^{2}+ 2}$

Explanation:

The expressions with can be separated from those with by multiplying both sides by $\frac{1}{y}\cdot \mathrm{d} x$ :

$\frac{\mathrm{d} y}{\mathrm{d} x} \cdot \frac{1}{y}\cdot \mathrm{d} x = \frac{xy}{x^{2}+ 2} \cdot \frac{1}{y}\cdot \mathrm{d} x$

$\frac{\mathrm{d} y}{y} = \frac{x \mathrm{\; d} x}{x^{2}+ 2}$

Find the indefinite integral of both sides:

$\int \frac{ \mathrm{d} y }{y}=\int \frac{x \mathrm{ \; d} x}{x^{2}+ 2 }$

$\ln y =\int \frac{x \mathrm{\; d} x}{x^{2}+ 2 }$

Set $u = x^{2}+ 2$ . Then $\mathrm{d} u = 2x \; \mathrm{ d} x$ , or $x \; \mathrm{ d} x =\frac{1}{2} \mathrm{d} u$ , and

$\ln y =\frac{1}{2}\int \frac{ { d} u}{u }$

$\ln y =\frac{1}{2} ( \ln u + C)$

$\ln y =\frac{1}{2} \ln u + C_{1}$

$\ln y = \ln \sqrt{u} + C_{1}$

Substitute back:

$\ln y = \ln \sqrt{ x^{2}+ 2} + C_{1}$ ;

Raise to both powers:

$\ln y = \ln \sqrt{ x^{2}+ 2} + C_{1}$

$e^{ \ln y }=e^{ \ln \sqrt{ x^{2}+ 2} + C_{1}}$

$y =C_{2}e^{ \ln \sqrt{ x^{2}+ 2} }$

$y =C_{2} \sqrt{ x^{2}+ 2}$ .

The correct choice is $y =C \sqrt{ x^{2}+ 2}$

Report an Error

Example Question #162 : Computation Of The Derivative

Find the derivative using the chain rule.

$\cos (3x^2)$

Possible Answers:

$-6x\sin (3x^2)$

$-6x\cos (3x^2)$

$6x\sin (3x^2)$

$6x\cos(3x^2)$

Correct answer:

$-6x\sin (3x^2)$

Explanation:

Use the chain rule to find the derivative: $\frac{d}{dx}f(g(x))=g'(x)f'(g(x))$

Thus, $\frac{d}{dx}\cos (3x^2)=-6x\sin (3x^2)$

Report an Error

Example Question #161 : Computation Of The Derivative

Find the derivative using the chain rule.

$\tan (5x)$

Possible Answers:

$5\sec (5x)$

$\sec^2(5x)$

$5\sec^2(5x)$

$\sec^2(5)$

Correct answer:

$5\sec^2(5x)$

Explanation:

Use the chain rule to find the derivative.

$\frac{d}{dx}\tan (5x)=5\sec^2(5x)$

Report an Error

Example Question #162 : Computation Of The Derivative

Find the derivative using the chain rule.

$\sin (-3x)$

Possible Answers:

$3\cos (3x)$

$-3\sin (-3x)$

$-3\cos (-3x)$

$3\sin (3x)$

Correct answer:

$-3\cos (-3x)$

Explanation:

Use the chain rule to find the derivative.

$\frac{d}{dx}\sin (-3x)=-3\cos (-3x)$

Report an Error

Example Question #163 : Computation Of The Derivative

Find the derivative using the chain rule.

$\cos (-2x)$

Possible Answers:

$-2\cos (-2x)$

$2\cos (-2x)$

$-2\sin (-2x)$

$2\sin (-2x)$

Correct answer:

$2\sin (-2x)$

Explanation:

Use the chain rule to find the derivative.

$\frac{d}{dx}\cos (-2x)=2\sin(-2x)$

Report an Error

Example Question #254 : Derivatives

$y+ \cos y = x^{2}$ .

Which of the following expressions is equal to $\frac{\mathrm{d} y}{\mathrm{d} x}$ ?

Possible Answers:

$\frac{\mathrm{d}y }{\mathrm{d} x}=\frac{2x}{1 + \tan y }$

$\frac{\mathrm{d}y }{\mathrm{d} x}=\frac{2x}{ \sin y -1 }$

$\frac{\mathrm{d}y }{\mathrm{d} x}=\frac{2x}{1 - \tan y }$

$\frac{\mathrm{d}y }{\mathrm{d} x}=\frac{2x}{1 - \sin y }$

$\frac{\mathrm{d}y }{\mathrm{d} x}=\frac{2x}{1 - \cos y }$

Correct answer:

$\frac{\mathrm{d}y }{\mathrm{d} x}=\frac{2x}{1 - \sin y }$

Explanation:

Differentiate both sides with respect to :

$y+ \cos y = x^{2}$

$\frac{\mathrm{d} }{\mathrm{d} x}(y+ \cos y )= \frac{\mathrm{d} }{\mathrm{d} x}(x^{2})$

$\frac{\mathrm{d} }{\mathrm{d} x}(y+ \cos y )=2x$

By the sum rule:

$\frac{\mathrm{d} }{\mathrm{d} x}(y )+ \frac{\mathrm{d} }{\mathrm{d} x}( \cos y ) =2x$

$\frac{\mathrm{d}y }{\mathrm{d} x} + \frac{\mathrm{d} }{\mathrm{d} x}( \cos y ) =2x$

By the chain rule:

$\frac{\mathrm{d}y }{\mathrm{d} x} + \frac{\mathrm{d} y}{\mathrm{d} x} \frac{\mathrm{d} }{\mathrm{d} y}( \cos y ) =2x$

$\frac{\mathrm{d}y }{\mathrm{d} x} + \frac{\mathrm{d} y}{\mathrm{d} x} \cdot (-\sin y) =2x$

Applying some algebra:

$\frac{\mathrm{d}y }{\mathrm{d} x} \left (1- \sin y \right ) =2x$

$\frac{\frac{\mathrm{d}y }{\mathrm{d} x} \left (1- \sin y \right )}{1 - \sin y } =\frac{2x}{1 - \sin y }$

$\frac{\mathrm{d}y }{\mathrm{d} x}=\frac{2x}{1 - \sin y }$

Report an Error

Example Question #74 : Chain Rule And Implicit Differentiation

$y^{2}- 4y + 8 = x$

Which of the following is equal to $\frac{\mathrm{d} y}{\mathrm{d} x}$ ?

Possible Answers:

$\frac{\mathrm{d} y}{\mathrm{d} x} =\frac{y}{ 2y - 4 }$

$\frac{\mathrm{d} y}{\mathrm{d} x} =\frac{x}{ y - 4 }$

$\frac{\mathrm{d} y}{\mathrm{d} x} =\frac{1}{ 2y - 4 }$

$\frac{\mathrm{d} y}{\mathrm{d} x} =\frac{x}{ 2y - 4 }$

$\frac{\mathrm{d} y}{\mathrm{d} x} =\frac{1}{ y - 4 }$

Correct answer:

$\frac{\mathrm{d} y}{\mathrm{d} x} =\frac{1}{ 2y - 4 }$

Explanation:

Differentiate both sides with respect to :

$y^{2}- 4y + 8 = x$

$\frac{\mathrm{d} }{\mathrm{d} x} (y^{2}- 4y + 8 )=\frac{\mathrm{d} }{\mathrm{d} x} (x)$

Apply the sum, difference, and constant multiple rules:

$\frac{\mathrm{d} }{\mathrm{d} x} (y^{2})- \frac{\mathrm{d} }{\mathrm{d} x} (4y )+\frac{\mathrm{d} }{\mathrm{d} x} ( 8 )=\frac{\mathrm{d} }{\mathrm{d} x} (x)$

In the first term, apply the chain rule; in the second, apply the constant multiple rule:

$\frac{\mathrm{d} y}{\mathrm{d} x} \cdot \frac{\mathrm{d} }{\mathrm{d} y} (y^{2})- 4 \frac{\mathrm{d} y}{\mathrm{d} x} +0=1$

Apply the power rule:

$\frac{\mathrm{d} y}{\mathrm{d} x} \cdot 2y - 4 \frac{\mathrm{d} y}{\mathrm{d} x} =1$

Now apply some algebra:

$( 2y - 4 )\frac{\mathrm{d} y}{\mathrm{d} x} =1$

$\frac{\mathrm{d} y}{\mathrm{d} x} =\frac{1}{ 2y - 4 }$

Report an Error

Example Question #165 : Computation Of The Derivative

We have three functions, g(x)=cos(x), h(x)=sin(x), k(x)=x^2

Find the derivative of f(x)

Given that f(x)=g(h(k(x)))

Possible Answers:

-sin(sin(x^2))*cos(2x)

sin(sin(x^2))*cos(x^2)

-sin(sin(x^2))*cos(x^2)*2x

-sin(cos(2x))

sin(sin(x^2))*cos(x^2)*2x

Correct answer:

-sin(sin(x^2))*cos(x^2)*2x

Explanation:

So now this is a three layer chain rule differentiation. The more functions combine to form the composite function the harder it will be to keep track of the derivative. I find it helpful to lay out each equation and each derivative, so:

g(x)=cos(x), g'(x)=-sin(x)

h(x)=sin(x), h'(x)=cos(x)

k(x)=x^2, k'(x)=2x

Then a three layer chain rule is just the same as a two layer, except... there's one more layer!

f'(x)=g'(h(k(x)))*h'(k(x))*k'(x)

It is still the outermost layer evaluated at the inner layers, and then move another layer in and repeat

Report an Error

View AP Calculus AB Tutors

Evgenii
Certified Tutor

View AP Calculus AB Tutors

Daniel
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Psychology.

View AP Calculus AB Tutors

Rachel
Certified Tutor

University of Arkansas at Little Rock, Bachelor in Arts, Mathematics.

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ISEE Tutors in Washington DC, ISEE Tutors in Denver, Algebra Tutors in Phoenix, Physics Tutors in Boston, French Tutors in Philadelphia, Statistics Tutors in San Francisco-Bay Area, Chemistry Tutors in Washington DC, Biology Tutors in Dallas Fort Worth, MCAT Tutors in Houston, Computer Science Tutors in New York City

Popular Courses & Classes

LSAT Courses & Classes in Los Angeles, ISEE Courses & Classes in Los Angeles, GMAT Courses & Classes in Los Angeles, ACT Courses & Classes in Denver, MCAT Courses & Classes in Washington DC, GRE Courses & Classes in Denver, GMAT Courses & Classes in Phoenix, SAT Courses & Classes in Boston, ISEE Courses & Classes in New York City, GMAT Courses & Classes in Chicago

Popular Test Prep

GMAT Test Prep in Boston, GRE Test Prep in Boston, ACT Test Prep in Dallas Fort Worth, GMAT Test Prep in Los Angeles, LSAT Test Prep in San Francisco-Bay Area, MCAT Test Prep in Houston, SAT Test Prep in San Francisco-Bay Area, GRE Test Prep in Dallas Fort Worth, LSAT Test Prep in Chicago, ISEE Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus AB : Computation of the Derivative

Study concepts, example questions & explanations for AP Calculus AB

All AP Calculus AB Resources

Example Questions

Example Question #61 : Chain Rule And Implicit Differentiation

Example Question #62 : Chain Rule And Implicit Differentiation

Example Question #161 : Computation Of The Derivative

Example Question #162 : Computation Of The Derivative

Example Question #161 : Computation Of The Derivative

Example Question #162 : Computation Of The Derivative

Example Question #163 : Computation Of The Derivative

Example Question #254 : Derivatives

Example Question #74 : Chain Rule And Implicit Differentiation

Example Question #165 : Computation Of The Derivative

All AP Calculus AB Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: