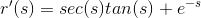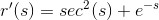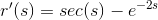We are going to use three rules along with the chain rule:

So then, using our first rule and the chain rule

then using our second rule and chain rule

then using our third rule (no chain rule this time)

Then we rearrange the equation for simplification,

We are going to use two rule and the chain rule

Then, using rule one and rule two (don't forget the chain rule)

Then we simplify

We will use the chain rule combined with our power rule:

Then by using this rule

Then applying the power rule to each element in the second parenthesis, 

We will be using the chain rule along with the following rules:

Looking at , first we will apply rule 3 with the chain rule,

Now we apply rule 1 (with chain rule) and rule 3 (no chain rule needed here),

Lastly we apply rule 2 (no chain rule needed),

Then we simplify as much as we can, and of course, what we have just calculated is the derivative of the original,

We will be using the following rule and the chain rule:

Also remember that

Now, looking at our function we are to find the derivative of,

We must use our first rule and the chain rule,

Let's rewrite that a little using our second rule,

Now let's use our first rule again (no further chain rule is required)

And now we just need to simplify,

So

We are going to use the following rules and the chain rule:

Now, looking at our original function,

can be written as

Then

Now we finish up by using the second rule backwards and then the first rule on the remainder (no more chain rule is required),

And finally, we have the derivative

Compute the derivative of the following function:

To find this derivative, we are going to use the chain rule:

What this means, is that we will take the derivative of the "outside" *in this case the  bit and keep the "inside" the same. Then we multiply all of this by the derivative of the inside.

So, let's jump in.

We can easily do our f' part. Doing so yields

Next, calculate the derivative of the inside.

Put that back together with the above part to get:

Clean it up a bit to get.

Which we will leave as...

*****************************************************************

                                          REQUIRED KNOWLEDGE

*****************************************************************

This problem requires us to understand two things:

1) The derivative of the function  is always  by itself

2) By adding an operation to the variable in the exponent (in our case, the -s instead of just s), we must multiply the derivative by the derivative of the argument in the exponent. This is an application of the chain rule of derivation

*****************************************************************

                                          SOLUTION STEPS

***************************************************************** is given 

Thus:

   The -1 comes from the derivative of -s

Thus, the correct answer is:

*****************************************************************

                                          CORRECT ANSWER

*****************************************************************

*****************************************************************

                                               PROBLEMS?

*****************************************************************

If you did not understand the concepts required to solve this derivative problem:

• Look into the derivative of e raised to an argument
• Practice applying the chain rule to derivative problems

*****************************************************************

                                                     STEPS

*****************************************************************

Given: 

Let:

Now:

Now, we plug in sin^2(x) again

To find "chain", we must take the derivative of sin^2(x), using the product rule:

Plug in this new-found term into the chain in the above derivative:

Canceling the sin on top with a sin on bottom, we arrive at the correct answer:

*****************************************************************

                                              CORRECT ANSWER

*****************************************************************

*****************************************************************

                                                    STEPS

*****************************************************************

Understand that if:

,

then:

Rearrange this as such:

We are also given:

Thus,

Plugging in 3dt into our previous dx allows us to look for dy/dt

Rearranging, we arrive at the correct answer:

*****************************************************************

                                           CORRECT ANSWER

*****************************************************************