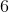The easiest way to approach this problem is to break it up into terms to get:

This simplifies to:

This then becomes a simple derivative in which you get:

Which after simplifying you get:

This is a derivative of sums with a trigonometric function thrown in there.

Upon simplifying you get:

Keeping in mind the derivative of cos(x) is -sin(x)

This is a product rule using trigonometric functions:

This can be simplified further:

What is in red cancels and you get:

But you can take this one step further and pull out a sin(x) to get:

The derivative of any term that does not include an "x" is zero. Therefore, the derivative of 7 is 0. The derivative of the second term follows if  then . The negative sign can be pulled out as a -1 coefficient before you differentiate. 

If a function is in the form of , then the derivative is .

To solve   you solve bring the 7 down in front of the x and lower the exponent by 1. 

This will bring you to the answer .

The apostrophe (') denotes that this is the first derivative of the function. 

Using the power rule which states,

you can move the  from  to the front and decrease the exponent by  which makes it .

For , any term that has an exponent of , the coefficient is its derivative.

Thus, the derivative of  is .

Since  does not have a variable attached, the derivative will be .

Add your derivatives to get .

Use the power rule to move the exponent of each term to the front, and multiply it with the existing coefficient to create the new coefficient for the derivative.

In mathematical terms, the power rule states,

Applying the power rule to the first term creates .

Next, move the  from  to the front and multiply it by , and decrease the exponent by 1 to get .

Next, since  does not have an exponent, the derivative of that will be .

Lastly,  has a derivative of  because there is not variable attached to it.

Therefore the derivative becomes, 

.

To find the derivative, use the power rule.

In mathematical terms, the power rule states,

 is the same as .

Therefore, move the exponent to the front, and then decrease it by one to get 

.

After simplifying, you get 

.

Having a binomial does not change the rules for the power rule. You still move the exponent to the front, and decrease the exponent by .

In mathematical terms, the power rule states,

Constants still have a derivative of  

Thus, giving you a final answer of 

Use the chain rule to move the exponent of the binomial to the front, and decrease the exponent by 1. Next, take the derivative of what is on the inside and multiply it with what is one the outside.

In mathematical terms the chain rule is,

Identify f(x) and its derivative first.

Substituting the function and its derivative into the chain rule formula, the final derivative becomes

Thus, giving you an answer of .