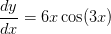All AP Calculus AB Resources
Example Questions
Example Question #201 : Computation Of The Derivative
Let ![f(x)=[e^{2x}+\sin(e^{x^3})]^3](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1040264/gif.latex)

The shortest and simplest way to find the derivative of this function is to use the Chain Rule. The Chain Rule definition is ![[f(g(x))]' = f'(g(x))\cdot g'(x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1040266/gif.latex)




Applying the chain rule to this pair of layers means applying the power rule to the outer function, then multiplying it by the derivative of the inner function. Doing so gives
We will need to find the derivative of the inner function, 

To find 
The derivative of 

The derivative of 




Putting these together we get the following for the derivative of
Simplifying it, we get
Putting this at the end of the original chain rule we have
This cannot be simplified, so it is the final answer
Example Question #202 : Computation Of The Derivative
Find 
According to the chain rule ![\frac{d}{du}[f(g(u))]=f'(g(u)) \cdot g'(u)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1044433/gif.latex)
Therefore, the derivative we are looking for will be
Example Question #203 : Computation Of The Derivative
Use implicit differentiation to calculate 
Differentiate both sides of the equation:
Simplify:
Use implicit differentiation to evaluate 
Simplify:
Subtract 
Divide both sides of the equation by siny:
Simplify:
Solution:
Example Question #1 : Derivative Rules For Sums, Products, And Quotients Of Functions
Find the derivative of the function,
Differentiate both sides and proceed with the product rule:
![\frac{dy}{dx}=\frac{d}{dx}[x^2\sin(3x)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/749291/gif.latex)
Evaluate the derivatives in each term. For the first term,

apply the chain rule,
So now the first term in equation (2) can be written,
![x^2\frac{d}{dx}\sin(3x)=x^2[3\cos(3x)]=3x^2\cos(3x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/741374/gif.latex)
The second term in equation (2) is easy, this is just the product of 


Combine equations (3) and (4) to write the derivative,
Example Question #681 : Ap Calculus Ab
Find the derivative.
Use the product rule to find the derivative.
Example Question #3 : Derivative Rules For Sums, Products, And Quotients Of Functions
Find the derivative.
Use the power rule to find the derivative.
Thus, the derivative is
Example Question #4 : Derivative Rules For Sums, Products, And Quotients Of Functions
Find 
Here we use the product rule:
Let 
Then 
and 
Subbing these values back into our equation gives us
Simplify by combining like-terms
and pulling out a 
Example Question #5 : Derivative Rules For Sums, Products, And Quotients Of Functions
If 

When evaluating the derivative, pay attention to the fact that 

and hence

Example Question #6 : Derivative Rules For Sums, Products, And Quotients Of Functions
If 
To obtain an expression for 


Substituting 

Example Question #2 : Derivative Rules For Sums, Products, And Quotients Of Functions
If 

To find 






All AP Calculus AB Resources

![f'(x)=3[e^{2x}+\sin(e^{x^3})]^2[e^{2x}+\cos(e^{x^3})]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1040257/gif.latex)

![f'(x)=[2e^{2x}+3x^2e^{x^3}\cos(e^{x^3})]^3](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1040259/gif.latex)
![f'(x)=3[e^{2x}+\sin(e^{x^3})]^2[2e^{2x}+3x^2e^{x^3}\cos(e^{x^3})]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1040256/gif.latex)










![\frac{d}{du}[sin(u)]=cos(u)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1044431/gif.latex)
![\frac{d}{du}[e^u]=e^u \cdot u'](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1044432/gif.latex)


















![\frac{dy}{dx} =x[3x\cos(3x)+2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/741367/gif.latex)