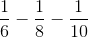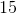We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : SSAT Upper Level Quantitative (Math)

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #5 : How To Find The Perimeter Of A Right Triangle

What is the perimeter of a right triangle with a hypotenuse of length and a leg of length ?

Possible Answers:

$8+ 2\sqrt{33}$

$22+ 2\sqrt{33}$

Not enough information provided

$2\sqrt{33}$

$14+ 2\sqrt{33}$

Correct answer:

$22+ 2\sqrt{33}$

Explanation:

In order to find the perimeter of the right triangle, we need to first find the missing length of the second leg. In order to find the second leg, use the Pythagorean Theorem:

$a^{2}+ b^{2}=c^{2}$ , where and are the lengths of the legs of the triangle, and is the length of the hypotenuse.

Substituting in our known values:

$8^{2}+ b^{2}=14^{2}$

Subtracting 8^2 from each side of the equation lets us isolate the variable for which we are solving:

$b^{2}=14^{2}-8^{2}$

$b^{2}=196-64$

$b^{2}=132$

$b=\sqrt{132}$

$b=\sqrt{33\times 4}$

$b=2\sqrt{33}$

Now that we have the lengths of all three sides of the right triangle, we can calculate the perimeter :

$P=14+8+2\sqrt{33}$

$P=22+2\sqrt{33}$

Report an Error

Example Question #6 : How To Find The Perimeter Of A Right Triangle

Find the perimeter of a right triangle with two legs of length and , respectively.

Possible Answers:

$8+4\sqrt{13}$

$12+4\sqrt{13}$

Not enough information provided

$20+4\sqrt{13}$

$4\sqrt{13}$

Correct answer:

$20+4\sqrt{13}$

Explanation:

In order to find the perimeter of the right triangle, we need to first find the missing length of the hypotenuse. In order to find the length of the hypotenuse, use the Pythagorean Theorem:

$a^{2}+ b^{2}=c^{2}$ , where and are the lengths of the legs of the triangle, and is the length of the hypotenuse.

Substituting in our known values:

$8^{2}+ 12^{2}=c^{2}$

$64+144=c^{2}$

$208=c^{2}$

$\sqrt{208}=c$

$\sqrt{13\times 16}=c$

$4\sqrt{13}=c$

Now that we have all three sides of the right triangle, we can calculate the perimeter:

$P=8+12+4\sqrt{13}$

$P=20+4\sqrt{13}$

Report an Error

Example Question #1 : Right Triangles

If a 3-4-5 right triangle is similar to a 6-8-10 right triangle, which of the other triangles must also be a similar triangle?

Possible Answers:

$\frac{1}{6}-\frac{1}{8}-\frac{1}{10}$

$\frac{1}{3}-\frac{1}{4}-\frac{1}{5}$

12-16-20

9-10-11

4-5-6

Correct answer:

12-16-20

Explanation:

For the triangles to be similar, the dimensions of all sides must have the same ratio by dividing the 3-4-5 triangle.

The 6-8-10 triangle will have a scale factor of 2 since all dimensions are doubled the original 3-4-5 triangle.

The only correct answer that will yield similar ratios is the 12-16-20 triangle with a scale factor of 4 from the 3-4-5 triangle.

The other answers will yield different ratios.

Report an Error

Example Question #4 : Shape Properties

What is the main difference between a right triangle and an isosceles triangle?

Possible Answers:

A right triangle has to have a $90^{\circ}$ angle and an isosceles triangle has to have equal, base angles.

An isosceles triangle has to have a $90^{\circ}$ angle and a right triangle has to have equal, base angles.

A right triangle has to have a $50^{\circ}$ angle and an isosceles triangle has to have equal, base angles.

A right triangle has to have a $90^{\circ}$ angle and an isosceles triangle has to have equal, base angles.

Correct answer:

A right triangle has to have a $90^{\circ}$ angle and an isosceles triangle has to have equal, base angles.

Explanation:

By definition, a right triangle has to have one right angle, or a $90^{\circ}$ angle, and an isosceles triangle has equal base angles and two equal side lengths.

Report an Error

Example Question #1 : How To Find The Length Of The Side Of A Right Triangle

A right triangle has a hypotenuse of 39 and one leg is 36. What is the length of the other leg?

Possible Answers:

Correct answer:

Explanation:

You may recognize these numbers as multiples of 13 and 12 (each by a factor of 3) and remember that sides of length 5, 12 and 13 make a special right triangle. So the other leg would be 15 $(5\times 3)$ .

If you don't remember this, you can use Pythagorean theorem:

$39^{2}-36^{2}= 1521-1296=225$

$\sqrt{225}=15$

Report an Error

Example Question #2 : How To Find The Length Of The Side Of A Right Triangle

A right triangle has a hypotenuse of and one leg has a length of . What is the length of the other leg?

Possible Answers:

$7\sqrt{3}$

$3\sqrt{7}$

Correct answer:

$3\sqrt{7}$

Explanation:

When calculating the lengths of sides of a right triangle, we can use the Pythagorean Theorem as follows:

$a^{2}+b^{2}=c^{2}$ , where and are legs of the triangle and is the hypotenuse.

Plugging in our given values:

$9^{2}+b^{2}=12^{2}$

Subtracting 9^2 from each side of the equation:

$b^{2}=12^{2}-9^{2}$

$b^{2}=144-81$

$b^{2}=63$

Taking the square root of each side of the equation:

$b=\sqrt{63}$

Simplifying the square root:

$b=\sqrt{9\times 7}$

$b=3\sqrt{7}$

Report an Error

Example Question #2 : How To Find The Length Of The Side Of A Right Triangle

A right triangle has two legs of length and , respectively. What is the hypotenuse of the right triangle?

Possible Answers:

$34\sqrt{2}$

$17\sqrt{2}$

$2\sqrt{34}$

$2\sqrt{17}$

Correct answer:

$2\sqrt{34}$

Explanation:

When calculating the lengths of sides of a right triangle, we can use the Pythagorean Theorem as follows:

$a^{2}+b^{2}=c^{2}$ , where and are legs of the triangle and is the hypotenuse.

Plugging in our given values:

$6^{2}+10^{2}=c^{2}$

$36+100=c^{2}$

$136=c^{2}$

$\sqrt{136}=c$

$\sqrt{17\times 8}=c$

$\sqrt{17\times 4\times 2}=c$

$2\sqrt{34}=c$

Report an Error

Example Question #1 : How To Find The Length Of The Side Of A Right Triangle

A right triangle has a leg of length and a hypotenuse of length . What is the length of the other leg?

Possible Answers:

$9\sqrt{6}$

$6\sqrt{2}$

$2\sqrt{6}$

$6\sqrt{9}$

Correct answer:

$6\sqrt{2}$

Explanation:

When calculating the lengths of sides of a right triangle, we can use the Pythagorean Theorem as follows:

$a^{2}+b^{2}=c^{2}$ , where and are legs of the triangle and is the hypotenuse.

Plugging in our given values:

$7^{2}+b^{2}=11^{2}$

Subtracting 7^2 from each side of the equation:

$b^{2}=11^{2}-7^{2}$

$b^{2}=121-49$

$b^{2}=72$

$b=\sqrt{72}$

$b=\sqrt{36\times 2}$

$b=6\sqrt{2}$

Report an Error

Example Question #2 : How To Find The Length Of The Side Of A Right Triangle

Find the length of the missing side.

Possible Answers:

160

$4\sqrt{10}$

$\sqrt{15}$

Correct answer:

$4\sqrt{10}$

Explanation:

Use the Pythagorean Theorem to find the length of the missing side.

x^2+6^2=14^2

x^2+36=196

x^2=160

$x=\sqrt{160}=4\sqrt{10}$

Report an Error

Example Question #671 : Ssat Upper Level Quantitative (Math)

Find the length of the missing side.

Possible Answers:

$8\sqrt2$

176

$4\sqrt{13}$

$4\sqrt{11}$

Correct answer:

$4\sqrt{11}$

Explanation:

Use the Pythagorean Theorem to find the length of the missing side.

x^2+7^2=15^2

x^2+49=225

x^2=176

$x=\sqrt{176}=4\sqrt{11}$

Report an Error

View SSAT- Upper Level Tutors

Rose
Certified Tutor

Texas A & M University-Corpus Christi, Associate in Science, Elementary School Teaching. Walden University, Masters in Educat...

View SSAT- Upper Level Tutors

Kevin
Certified Tutor

St. Johns University, Bachelors, Math/Coaching.

View SSAT- Upper Level Tutors

Joseph
Certified Tutor

Bank Street College of Education , Master's/Graduate, Early Childhood and Childhood General Education.

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Math Tutors in Dallas Fort Worth, Chemistry Tutors in Atlanta, Calculus Tutors in Denver, ISEE Tutors in San Diego, Biology Tutors in Phoenix, Biology Tutors in San Diego, LSAT Tutors in Los Angeles, SAT Tutors in Chicago, Statistics Tutors in Atlanta, SAT Tutors in Philadelphia

Popular Courses & Classes

GRE Courses & Classes in Seattle, LSAT Courses & Classes in New York City, ISEE Courses & Classes in Boston, ISEE Courses & Classes in San Diego, ACT Courses & Classes in Miami, SAT Courses & Classes in Denver, ISEE Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Denver, ACT Courses & Classes in New York City, MCAT Courses & Classes in Atlanta

Popular Test Prep

ISEE Test Prep in Los Angeles, ACT Test Prep in New York City, MCAT Test Prep in Seattle, MCAT Test Prep in New York City, LSAT Test Prep in New York City, ISEE Test Prep in Denver, ACT Test Prep in Miami, ISEE Test Prep in San Francisco-Bay Area, ISEE Test Prep in Washington DC, GRE Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : SSAT Upper Level Quantitative (Math)

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #5 : How To Find The Perimeter Of A Right Triangle

Example Question #6 : How To Find The Perimeter Of A Right Triangle

Example Question #1 : Right Triangles

Example Question #4 : Shape Properties

Example Question #1 : How To Find The Length Of The Side Of A Right Triangle

Example Question #2 : How To Find The Length Of The Side Of A Right Triangle

Example Question #2 : How To Find The Length Of The Side Of A Right Triangle

Example Question #1 : How To Find The Length Of The Side Of A Right Triangle

Example Question #2 : How To Find The Length Of The Side Of A Right Triangle

Example Question #671 : Ssat Upper Level Quantitative (Math)

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: