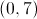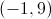We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : SSAT Upper Level Quantitative (Math)

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #6 : How To Graph Inverse Variation

The graphs of the equations $y = \frac{3}{x}$ and 4x-2y = -10 intersect in two points; one has a positive -coordinate. and one has a negative -coordinate. Give the -coordinate of the point of intersection that has a positive -coordinate.

Possible Answers:

Correct answer:

Explanation:

Substitute $\frac{3}{x}$ for in the second equation:

4x-2y = -10

$4x-2 \left ( \frac{3}{x} \right )= -10$

$4x- \frac{6}{x} = -10$

$4x- \frac{6}{x} + 10 = -10+ 10$

$4x- \frac{6}{x} + 10 = 0$

$\left (4x- \frac{6}{x} + 10 \right ) \cdot \frac{x}{2} = 0 \cdot \frac{x}{2}$

$2x^{2}-3+5x = 0$

$2x^{2}+5x -3= 0$

This quadratic equation can be solved using the method; the integers with product $2 \cdot (-3) = -6$ and sum 5 are and 6, so continue as follows:

$2x^{2}-x+6x -3= 0$

x (2x -1) +3(2x -1)= 0

(x+3 )(2x -1)= 0

Either x+3 = 0 , in which case x = -3 , or

2x-1 = 0 , in which case

2x = 1

x = 0.5

The desired -coordinate is paired with the positive -coordinate, so we substitute 0.5 for in the first equation:

$y = \frac{3}{x} = \frac{3}{0.5} = 6$

Report an Error

Example Question #5 : How To Graph Inverse Variation

Give the -coordinate of the point at which the graphs of the equations $y = \frac{2}{x}$ and $y = -\frac{3}{x+1}$ intersect.

Possible Answers:

The graphs of the equations do not intersect.

Correct answer:

Explanation:

Using the substitution method, set the values of equal to each other.

$\frac{2}{x} = -\frac{3}{x+1}$

Multiply both sides by $\frac{x(x+1)}{1}$ :

$\frac{2}{x} \cdot \frac{x(x+1)}{1}= -\frac{3}{x+1}\cdot \frac{x(x+1)}{1}$

2(x+1)= -3x

2x+2= -3x

2x+2 + 3x -2 = -3x + 3x -2

5x = -2

$5x \div 5 = -2 \div 5$

x = -0.4

Substitute in either equation:

$y = \frac{2}{x} = \frac{2}{-0.4} = -5$

Report an Error

Example Question #6 : How To Graph Inverse Variation

A line with slope 4 shares its -intercept with that of the graph of the equation $y = \frac{3}{2x-7}$ . Which of the following is the equation of that line?

Possible Answers:

This line does not exist, since the graph of $y = \frac{3}{2x-7}$ has no -intercept.

8x-2y =- 7

28x-7y=2

8x-2y=-3

28x-7y=3

Correct answer:

28x-7y=3

Explanation:

The -intercept of the graph of $y = \frac{3}{2x-7}$ —the point at which it crosses the -axis—is the point at which x = 0 , so substitute accordingly and solve for :

$y = \frac{3}{2 \cdot 0-7}= \frac{3}{ 0-7}=- \frac{3}{ 7}$

The -intercept of this graph, and that of the line, is $\left (0, - \frac{3}{ 7} \right )$ . Since the slope is 4, the slope-intercept form of the equation of the line is

$y = 4x-\frac{3}{7}$

To put it in standard form:

$y-y + \frac{3}{7} = 4x-\frac{3}{7} -y + \frac{3}{7}$

$\frac{3}{7} = 4x -y$

$\frac{3}{7} \cdot 7 = (4x -y) \cdot 7$

28x-7y=3

Report an Error

Example Question #7 : How To Graph Inverse Variation

$\bigtriangleup ABC \cong \bigtriangleup DEF$ , where $\angle B$ is a right angle, $m \angle C = 30 ^{\circ }$ , and AC = 30 . Which of the following cannot be true?

Possible Answers:

All of the statements given in the other choices are true.

$\angle F$ is a right angle

$m \angle D = 60^{\circ }$

$\bigtriangleup DEF$ has perimeter $45+15 \sqrt{3}$

DE= 15

Correct answer:

$\angle F$ is a right angle

Explanation:

$\angle B$ is a right angle and $m \angle C = 30 ^{\circ }$ , so

$m \angle A = 90 ^{\circ } - m \angle C = 90 ^{\circ } - 30 ^{\circ }= 60 ^{\circ }$ ,

making $\bigtriangleup ABC$ a 30-60-90 triangle. By the 30-60-90 Triangle Theorem, the length of the short leg $\overline{AB}$ is half that of hypotenuse $\overline{AC}$ :

$AB= \frac{1}{2}\cdot AC = \frac{1}{2}\cdot 30 = 15$

and the length of long leg $\overline{BC}$ is $\sqrt {3}$ times that of $\overline{AB}$ :

$BC = AB \cdot \sqrt{3}= 15 \cdot \sqrt{3}$

Corresponding sides of congruent triangles are congruent, so DE = AB ; since AB=15 , it follows that DE = 15 .

Also, DE = AB = 15 , $EF= BC = 15 \sqrt{3}$ , and DF = AC = 30 , so the perimeter of $\bigtriangleup DEF$ is the sum of these, or

$DE+EF+DF = 15+15 \sqrt{3}+30=45+15 \sqrt{3}$ .

Corresponding angles are congruent, so $m \angle D = m \angle A$ and $m \angle F = m \angle C$ . By substitution, $m \angle D = 60 ^{\circ }$ and $m \angle F = 30 ^{\circ }$ .

The false statement among the choices is that $\angle F$ is a right angle.

Report an Error

Example Question #261 : Coordinate Plane

What is the vertex of the function $f(x)=-2x^{2}-4x+7$ ?

Possible Answers:

(-2,7)

(1,1)

(2,-9)

(-1,9)

(0,7)

Correct answer:

(-1,9)

Explanation:

f(x)=ax^2+bx+c

$f(x)=-2x^{2}-4x+7$

The -coordinate of the vertex is $x=-\frac{b}{2a}$ , where a = -2, b=-4 .

$x=-\frac{b}{2a} = -\frac{-4}{2 \left (-2 \right )} = -1$

To get the -coordinate, evaluate f (-1) .

$f(x)=-2x^{2}-4x+7$

$f(1)=-2 \left (-1 \right )^{2}-4\left (-1 \right )+7 =-2+4+7=9$

The vertex is (-1,9) .

Report an Error

Example Question #1 : Properties Of Parallel And Perpendicular Lines

Line P passes through the origin and point $\left ( \frac{1}{9} , \frac{1}{7}\right )$ .

Line Q passes through the origin and point $\left ( \frac{1}{9} , -\frac{1}{7}\right )$ .

Line R passes through the origin and point $\left (\frac{1}{7}, \frac{1}{9} \right )$ .

Line S passes through the origin and point $\left (\frac{1}{7}, -\frac{1}{9} \right )$ .

Which of these lines is parallel to the line of the equation 7x+9y = 111 ?

Possible Answers:

Line P

Line Q

Line S

Line R

None of the other responses is correct.

Correct answer:

Line S

Explanation:

First, find the slope of the line of the equation 7x+9y = 111 by rewriting it in slope-intercept form:

7x+9y = 111

9y =-7x+ 111

$y =\frac{1}{9} \left (-7x+ 111 \right )$

$y = -\frac{7}{9}x+ \frac{111 }{9}$

The slope of this line is $-\frac{7}{9}$ , so we are looking for a line which also has this slope.

Find the slopes of all four lines by using the slope formula $m= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}$ . Since each line passes through the origin, this formula can be simplified to

$m= \frac{y_{2}-0}{x_{2}-0} = \frac{y_{2} }{x_{2} }$

using the other point.

Line P:

$m = \frac{y_{2} }{x_{2} }= \frac{ \frac{1}{7} }{ \frac{1}{9}} = \frac{1}{7} \div \frac{1}{9}= \frac{1}{7} \cdot \frac{9} {1} = \frac{9}{7}$

Line Q:

$m = \frac{y_{2} }{x_{2} }= \frac{- \frac{1}{7} }{ \frac{1}{9}} =- \frac{1}{7} \div \frac{1}{9}= -\frac{1}{7} \cdot \frac{9} {1} =- \frac{9}{7}$

Line R:

$m = \frac{y_{2} }{x_{2} }= \frac{ \frac{1}{9} }{ \frac{1}{7}} = \frac{1}{9} \div \frac{1}{7}= \frac{1}{9} \cdot \frac{7} {1} = \frac{7}{9}$

Line S:

$m = \frac{y_{2} }{x_{2} }= \frac{- \frac{1}{9} }{ \frac{1}{7}} = -\frac{1}{9} \div \frac{1}{7}=- \frac{1}{9} \cdot \frac{7} {1} =-\frac{7}{9}$

Line S has the desired slope and is the correct choice.

Report an Error

Example Question #2 : Properties Of Parallel And Perpendicular Lines

You are given three lines as follows:

Line A includes points (3, 8) and (1, 12) .

Line B includes point (6, 7) and has -intercept (0, 17) .

Line C includes the origin and point (4, -8) .

Which lines are parallel?

Possible Answers:

$\text{No two of Lines A, B, and C are parallel.}$

$\text{All three of Lines A, B, and C are parallel.}$

$\text{Only Lines A and B are parallel.}$

$\text{Only Lines A and C are parallel.}$

$\text{Only Lines B and C are parallel.}$

Correct answer:

$\text{Only Lines A and C are parallel.}$

Explanation:

Find the slope of all three lines using the slope formula $m= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}$ :

Line A:

$m= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}$

$m= \frac{12-8}{1-3} = \frac{4}{-2} = -2$

Line B:

$m= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}$

$m= \frac{7-17}{6-0} = \frac{-10}{6} = -\frac{5}{3}$

Line C:

$m= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}$

$m= \frac{-8-0}{4-0}= \frac{-8}{4} = -2$

Lines A and C have the same slope; Line B has a different slope. Only Lines A and C are parallel.

Report an Error

Example Question #641 : Ssat Upper Level Quantitative (Math)

Line A has equation 5x-7y = 20 .

Line B has equation 7x-5y = 32 .

Which statement is true of the two lines?

Possible Answers:

$\text{The lines are parallel.}$

$\text{The lines are identical.}$

$\text{The lines are perpendicular.}$

$\text{None of the other four statements are true.}$

$\text{The lines are different but neither parallel nor perpendicular.}$

Correct answer:

$\text{The lines are different but neither parallel nor perpendicular.}$

Explanation:

Write each statement in slope-intercept form:

Line A:

5x-7y = 20

-7y = -5x+ 20

$y =-\frac{1}{7}\left ( -5x+ 20 \right )$

$y = \frac{5}{7} x-\frac{ 20}{7}$

The slope is $\frac{5}{7}$ .

Line B:

7x-5y = 32

-5y = - 7x+ 32

$y = -\frac{1}{5 }\left ( - 7x+ 32 \right )$

$y = \frac{7}{5}x-\frac{32}{5}$

The slope is $\frac{7}{5}$ .

The lines have differing slopes, so they are neither identical nor parallel. The product of the slopes is $\frac{5}{7} \times \frac{7}{5} = 1 \ne -1$ , so they are not perpendicular. The correct response is that they are distinct lines that are neither parallel nor perpendicular.

Report an Error

Example Question #4 : Properties Of Parallel And Perpendicular Lines

Parallel

Figure NOT drawn to scale

In the above figure, m ||n . Evaluate .

Possible Answers:

x = 168

x = 114

x = 144

x = 132

Correct answer:

x = 132

Explanation:

Angles of degree measures and 3y - 12 form a linear pair, making the angles supplementary - that is, their degree measures total 180. Therefore,

y + (3y - 12) = 180

Solving for :

4 y - 12 = 180

4 y - 12 + 12 = 180 + 12

4y = 192

$4y \div 4 = 192 \div 4$

y = 48

The angles of measures and 3y - 12 form a pair of alternating interior angles of parallel lines, so, as a consequence of the Parallel Postulate, they are congruent, and

x = 3y - 12

Substituting for :

x = 3(48) - 12 = 144 - 12 = 132

Report an Error

Example Question #1 : Properties Of Parallel And Perpendicular Lines

Parallel

Figure NOT drawn to scale

In the above figure, m ||n . Express in terms of .

Possible Answers:

y = 48-x

y = 138 - x

y = x-14

y = x+42

Correct answer:

y = 138 - x

Explanation:

The two marked angles are same-side interior angles of two parallel lines formed by a transversal ; by the Parallel Postulate, the angles are supplementary - the sum of their measures is 180 degrees. Therefore,

(y+28 )+ ( x+ 14) = 180

x+y + 42 = 180

Solve for by moving the other terms to the other side and simplifying:

x+y + 42- 42 - x = 180 - 42 - x

y = 138 - x

Report an Error

View SSAT- Upper Level Tutors

Rose
Certified Tutor

Texas A & M University-Corpus Christi, Associate in Science, Elementary School Teaching. Walden University, Masters in Educat...

View SSAT- Upper Level Tutors

Kevin
Certified Tutor

St. Johns University, Bachelors, Math/Coaching.

View SSAT- Upper Level Tutors

Joseph
Certified Tutor

Bank Street College of Education , Master's/Graduate, Early Childhood and Childhood General Education.

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Statistics Tutors in San Diego, Physics Tutors in New York City, GMAT Tutors in Washington DC, SAT Tutors in Chicago, GMAT Tutors in Dallas Fort Worth, French Tutors in Denver, SSAT Tutors in Atlanta, Chemistry Tutors in Seattle, GMAT Tutors in San Francisco-Bay Area, Reading Tutors in Los Angeles

Popular Courses & Classes

ACT Courses & Classes in Chicago, GRE Courses & Classes in Seattle, SSAT Courses & Classes in Philadelphia, ISEE Courses & Classes in Washington DC, ISEE Courses & Classes in Atlanta, SSAT Courses & Classes in Seattle, LSAT Courses & Classes in New York City, SAT Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in Denver, ISEE Courses & Classes in San Diego

Popular Test Prep

GRE Test Prep in Boston, SSAT Test Prep in San Diego, MCAT Test Prep in Dallas Fort Worth, MCAT Test Prep in Chicago, LSAT Test Prep in New York City, ISEE Test Prep in San Diego, SAT Test Prep in San Francisco-Bay Area, ACT Test Prep in Boston, GRE Test Prep in Miami, ACT Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : SSAT Upper Level Quantitative (Math)

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #6 : How To Graph Inverse Variation

Example Question #5 : How To Graph Inverse Variation

Example Question #6 : How To Graph Inverse Variation

Example Question #7 : How To Graph Inverse Variation

Example Question #261 : Coordinate Plane

Example Question #1 : Properties Of Parallel And Perpendicular Lines

Example Question #2 : Properties Of Parallel And Perpendicular Lines

Example Question #641 : Ssat Upper Level Quantitative (Math)

Example Question #4 : Properties Of Parallel And Perpendicular Lines

Example Question #1 : Properties Of Parallel And Perpendicular Lines

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: