We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : SSAT Upper Level Quantitative (Math)

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

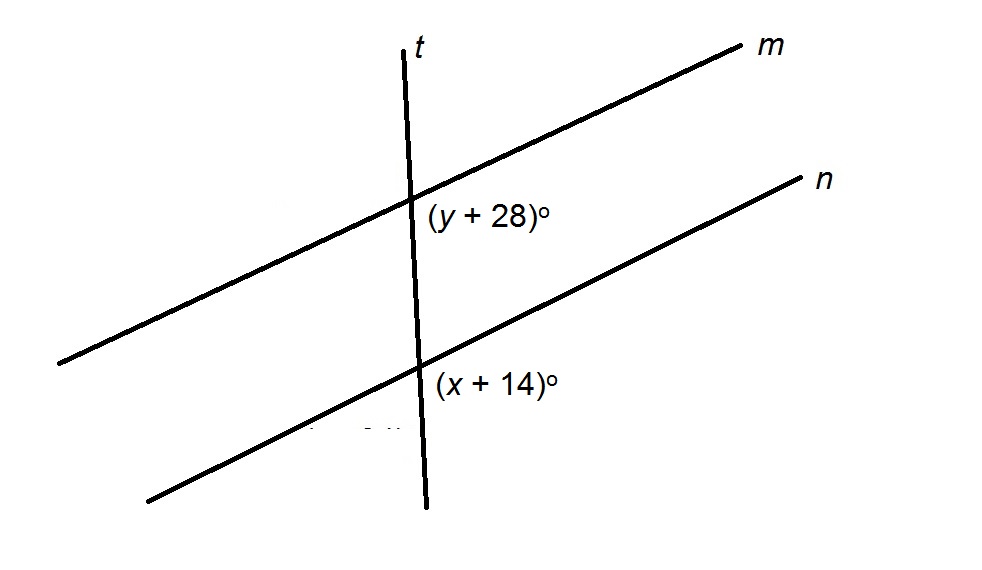
Example Question #1 : How To Find Whether Lines Are Parallel

Parallel

Figure NOT drawn to scale

In the above figure, m ||n . Express in terms of .

Possible Answers:

y = 48-x

y = 138 - x

y = x+42

y = x-14

Correct answer:

y = x-14

Explanation:

The two marked angles are corresponding angles of two parallel lines formed by a transversal, so the angles are congruent. Therefore,

y+28 = x+ 14

Solving for by subtracting 28 from both sides:

y+28 - 28 = x+ 14 - 28

y = x-14

Report an Error

Example Question #4 : How To Find Whether Lines Are Parallel

Parallel

Figure NOT drawn to scale

In the above figure, m ||n . Evaluate .

Possible Answers:

x = 106

x = 111

x = 101

x= 96

Correct answer:

x = 101

Explanation:

The two marked angles are same-side exterior angles of two parallel lines formed by a transversal ,; by the Parallel Postulate, the angles are supplementary - the sum of their measures is 180 degrees. Therefore,

(x+12) + (x- 34) = 180

2x -22 = 180

2x = 202

x = 101

Report an Error

Example Question #651 : Ssat Upper Level Quantitative (Math)

Three lines are drawn on the coordinate plane.

The green line has slope $\frac{2}{3}$ , and -intercept $\frac{4}{5}$ .

The blue line has slope $\frac{3}{2}$ , and -intercept $-\frac{5}{4}$ .

The red line has slope $-\frac{2}{3}$ , and -intercept $-\frac{4}{5}$ .

Which two lines are perpendicular to each other?

Possible Answers:

It cannot be determined from the information given.

No two of these lines are perpendicular.

The blue line and the green line are perpendicular.

The green line and the red line are perpendicular.

The blue line and the red line are perpendicular.

Correct answer:

The blue line and the red line are perpendicular.

Explanation:

To demonstrate two perpendicular lines, multiply their slopes; if their product is , then the lines are perpendicular (the -intercepts are irrelevant).

The products of these lines are given here.

Blue and green lines: $\frac{2}{3} * \frac{3}{2} = 1$

Red and green lines: $\frac{2}{3} * \left - \frac{2}{3} \right = -\frac{4}{9}$

Blue and red lines: $\frac{2}{3}* \left - \frac{3}{2} \right = -1$

It is the blue and red lines that are perpendicular.

We can also see that their slopes are negative reciprocals, indicating perpendicular lines.

Report an Error

Example Question #652 : Ssat Upper Level Quantitative (Math)

Two perpendicular lines intersect at point (3,8) . One line also includes point (4,-1) . What is the slope of the other line?

Possible Answers:

Insufficient information is given to answer the question.

$-\frac{1}{9}$

$\frac{1}{9}$

Correct answer:

$\frac{1}{9}$

Explanation:

The slopes of two perpendicular lines are the opposites of each other's reciprocals.

To find the slope of the first line substitute $x_{1} = 3, y_{1} =8, x_{2} = 4, y_{2} =-1$ in the slope formula:

$m =\frac{ y_{1}-y_{2}}{ x_{1}-x_{2}}$

$m =\frac{ 8 - (-1)}{ 3-4} = \frac{ 9}{ -1} = -9$

The slope of the first line is , so the slope of the second line is the opposite reciprocal of this, which is $\frac{1}{9}$ .

Report an Error

Example Question #653 : Ssat Upper Level Quantitative (Math)

Two perpendicular lines intersect at the origin; one line also passes through point (5,7) . What is the slope of the other line?

Possible Answers:

$\frac{ 7}{5}$

Insufficient information is given to solve the problem.

$-\frac{5}{ 7}$

$-\frac{ 7}{5}$

$\frac{5}{ 7}$

Correct answer:

$-\frac{5}{ 7}$

Explanation:

The slopes of two perpendicular lines are the opposites of each other's reciprocals.

To find the slope of the first line, substitute $x_{1} = 5, y_{1} =7, x_{2} = 0, y_{2} =0$ in the slope formula:

$m =\frac{ y_{1}-y_{2}}{ x_{1}-x_{2}}$

$m =\frac{ 7-0}{5-0}=\frac{ 7}{5}$

The slope of the first line is $\frac{ 7}{5}$ , so the slope of the second line is the opposite reciprocal of this, which is $-\frac{5}{ 7}$ .

Report an Error

Example Question #654 : Ssat Upper Level Quantitative (Math)

Which of the following lines is perpendicular to the line 3x-5y=11 ?

Possible Answers:

3x+5y=-11

9y+15x-54=0

3y-5x=-3

5y+3x=2

10y-6x+5=0

Correct answer:

9y+15x-54=0

Explanation:

All we care about for this problem is the slopes of the lines...the x- and y-intercepts are irrelevant.

Remember that the slopes of perpendicular lines are opposite reciprocals. By putting the given equation into y=mx+b form, we can see that its slope is $\frac{3}{5}$ . So we are looking for a line with a slope of $-\frac{5}{3}$ .

The equation 9y+15x-54=0 can be put into the form $y=-\frac{5}{3}x+6$ , and so we know that it is perpendicular to the given line.

Report an Error

Example Question #3 : How To Find Whether Lines Are Perpendicular

Line A passes through the origin and (8, 6) .

Line B passes through the origin and $\left ( -36, 64\right )$ .

Line C passes through the origin and $\left ( \frac{1}{12},- \frac{1}{16} \right )$ .

Line D passes through the origin and (0.9, -1.2) .

Line E passes through the origin and $\left ( \sqrt{2},-\sqrt{3} \right )$ .

Which line is perpendicular to Line A?

Possible Answers:

Line C

None of the other lines is perpendicular to A.

Line E

Line D

Line B

Correct answer:

Line D

Explanation:

Find the slopes of all five lines using the slope formula $m= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}$ . Since each line passes through the origin, this formula can be simplified to

$m= \frac{y_{2}-0}{x_{2}-0} = \frac{y_{2} }{x_{2} }$

using the other point.

Line A:

$m = \frac{6 }{8 } = \frac{3}{4}$

The correct line must have as its slope the opposite of the reciprocal of this, which is $m = -\frac{4}{3}$ .

Line B:

$m = \frac{64 }{-36}= - \frac{16}{9}$

Line C:

$m = \frac{ -\frac{1}{16} }{ \frac{1}{12}} = -\frac{1}{16} \div \frac{1}{12} = -\frac{1}{16} \cdot \frac{12} {1}= -\frac{12}{16} = -\frac{3}{4}$

Line D:

$m = \frac{-1.2 }{0.9 } = -\frac{12}{9} = -\frac{4}{3}$

Line E:

$m = \frac{ - \sqrt{3}}{ \sqrt{2} } = -\frac{\sqrt{6}}{2}$

Of the last four lines, only Line D has the desired slope.

Report an Error

Example Question #6 : How To Find Whether Lines Are Perpendicular

Line W passes through the origin and point $\left (\frac{1}{4}, \frac{1}{9} \right )$ .

Line X passes through the origin and point $\left (\frac{1}{4}, -\frac{1}{9} \right )$ .

Line Y passes through the origin and point $\left ( \frac{1}{9} , \frac{1}{4}\right )$ .

Line Z passes through the origin and point $\left ( \frac{1}{9} , -\frac{1}{4}\right )$ .

Which of these lines is perpendicular to the line of the equation 4x-9y = 100 ?

Possible Answers:

Line W

None of the other responses is correct.

Line X

Line Z

Line Y

Correct answer:

Line Z

Explanation:

First, find the slope of the line of the equation 4x-9y = 100 by rewriting it in slope-intercept form:

4x-9y = 100

-9y = -4x+100

$y =-\frac{1}{9} \left (-4x+100 \right )$

$y = \frac{4}{9} x-\frac{100 }{9}$

The slope of this line is $\frac{4}{9}$ , so we are looking for a line whose slope is the opposite of the reciprocal of this, or $-\frac{9}{4}$ .

Find the slopes of all four lines by using the slope formula $m= \frac{y_{2}-y_{1}}{x_{2}-x_{1}}$ . Since each line passes through the origin, this formula can be simplified to

$m= \frac{y_{2}-0}{x_{2}-0} = \frac{y_{2} }{x_{2} }$

using the other point.

Line W:

$m = \frac{y_{2} }{x_{2} }= \frac{ \frac{1}{9} }{ \frac{1}{4}} = \frac{1}{9} \div \frac{1}{4}= \frac{1}{9} \cdot \frac{4} {1} = \frac{4}{9}$

Line X:

$m = \frac{y_{2} }{x_{2} }= \frac{ - \frac{1}{9} }{ \frac{1}{4}} =- \frac{1}{9} \div \frac{1}{4}= -\frac{1}{9} \cdot \frac{4} {1} =- \frac{4}{9}$

Line Y:

$m = \frac{y_{2} }{x_{2} }= \frac{ \frac{1}{4} }{ \frac{1}{9}} = \frac{1}{4} \div \frac{1}{9}= \frac{1}{4} \cdot \frac{9} {1} = \frac{9}{4}$

Line Z:

$m = \frac{y_{2} }{x_{2} }= \frac{ -\frac{1}{4} }{ \frac{1}{9}} =-\frac{1}{4} \div \frac{1}{9}= -\frac{1}{4} \cdot \frac{9} {1} = -\frac{9}{4}$

Line Z has the desired slope and is the correct choice.

Report an Error

Example Question #7 : How To Find Whether Lines Are Perpendicular

Determine whether the two equations are parallel, perpendicular or neither, and choose the best reason.

$-2x+6y = 3 \textup{ and } -\frac{y}{3}=1$

Possible Answers:

Perpendicular, the slopes are the negative reciprocal to each other.

Parallel, the slopes are the same.

Neither, the slopes have no correlation.

Parallel, the slopes are the negative reciprocal to each other.

Perpendicular, the slopes are the same.

Correct answer:

Neither, the slopes have no correlation.

Explanation:

Convert both equations to slope intercept form: y=mx+b

-2x+6y = 3

6y =2x+3

$y=\frac{1}{3}x+\frac{1}{2}$

The slope of the first equation is $m_1=\frac{1}{3}$ .

Convert the second equation.

$-\frac{y}{3}=1$

y=-3

The slope of this equation is zero since there is no term! m_2=0

In order for the two functions to be parallel, they must have the same slopes.

In order for the two functions to be perpendicular, their slopes must be the negative reciprocal to each other.

Since there's no correlation with both slopes, the equations are neither parallel or perpendicular to each other.

The correct answer is:

Neither, the slopes have no correlation

Report an Error

Example Question #6 : How To Find Whether Lines Are Perpendicular

Given: the following three lines on the coordinate plane:

Line 1: The line of the equation x = 7

Line 2: The line of the equation y = 7

Line 3: The line of the equation x+y=7

Which of the following is a true statement?

Possible Answers:

Line 1 and Line 2 are perpendicular; Line 3 is perpendicular to neither.

None of the other responses is correct.

Line 1 and Line 3 are perpendicular; Line 2 is perpendicular to neither.

Line 2 and Line 3 are perpendicular; Line 1 is perpendicular to neither.

No two of Line 1, Line 2, or Line 3 form a pair of perpendicular lines.

Correct answer:

Line 1 and Line 2 are perpendicular; Line 3 is perpendicular to neither.

Explanation:

Line 1, the line of the equation x = 7 , is a vertical line on the coordinate plane; Line 2, the line of the equation y = 7 , is a horizontal line. Lines 1 and 2 are perpendicular to each other.

The slope of Line 3, the line of the equation x+y=7 , can be calculated by putting the equation in slope-intercept form:

x+y=7

x+y-x=7 - x

y = -1x+7

The slope is , which makes it perpendicular to a line of slope $-\frac{1}{-1} = 1$ . Line 1, being vertical, has undefined slope, and Line 2, being horizontal, has slope 0.

Correct response: Line 1 and Line 2 are perpendicular; Line 3 is perpendicular to neither.

Report an Error

View SSAT- Upper Level Tutors

Rose
Certified Tutor

Texas A & M University-Corpus Christi, Associate in Science, Elementary School Teaching. Walden University, Masters in Educat...

View SSAT- Upper Level Tutors

Kevin
Certified Tutor

St. Johns University, Bachelors, Math/Coaching.

View SSAT- Upper Level Tutors

Joseph
Certified Tutor

Bank Street College of Education , Master's/Graduate, Early Childhood and Childhood General Education.

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ISEE Tutors in Atlanta, Statistics Tutors in Boston, Biology Tutors in Seattle, ACT Tutors in Chicago, ACT Tutors in Phoenix, LSAT Tutors in Miami, GRE Tutors in Philadelphia, Reading Tutors in Denver, Spanish Tutors in Philadelphia, Reading Tutors in Dallas Fort Worth

Popular Courses & Classes

ACT Courses & Classes in Phoenix, Spanish Courses & Classes in New York City, GMAT Courses & Classes in Los Angeles, Spanish Courses & Classes in Los Angeles, GMAT Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Los Angeles, MCAT Courses & Classes in Denver, ISEE Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Washington DC

Popular Test Prep

GRE Test Prep in Miami, MCAT Test Prep in Miami, ISEE Test Prep in Houston, LSAT Test Prep in Houston, ISEE Test Prep in Boston, GRE Test Prep in New York City, MCAT Test Prep in Washington DC, GMAT Test Prep in Philadelphia, SAT Test Prep in Atlanta, SAT Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : SSAT Upper Level Quantitative (Math)

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #1 : How To Find Whether Lines Are Parallel

Example Question #4 : How To Find Whether Lines Are Parallel

Example Question #651 : Ssat Upper Level Quantitative (Math)

Example Question #652 : Ssat Upper Level Quantitative (Math)

Example Question #653 : Ssat Upper Level Quantitative (Math)

Example Question #654 : Ssat Upper Level Quantitative (Math)

Example Question #3 : How To Find Whether Lines Are Perpendicular

Example Question #6 : How To Find Whether Lines Are Perpendicular

Example Question #7 : How To Find Whether Lines Are Perpendicular

Example Question #6 : How To Find Whether Lines Are Perpendicular

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: