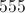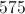A square pyramid has one square base and four triangular sides.

Vertices (where two or more edges come together):  5. There are four vertices on the base (one at each corner of the square) and a fifth at the top of the pyramid.

Edges (where two faces come together):  8. There are four edges on the base (one along each side) and four more along the sides of the triangular faces extending from the corners of the base to the top vertex.

Faces (planar surfaces):  5. The base is one face, and there are four triangular faces that form the top of the pyramid.

Total

Volume of Pyramid = 1/3 * Area of Base * Height

12,000 ft³ = 1/3 * 30ft * 30ft * H

12,000  = 300 * H

H = 12,000  / 300 = 40

H = 40 ft

Volume of a pyramid is

Thus:

Area of the base is .

Therefore, each side is .

To find the surface area of a pyramid we must add the areas of all five of the shapes creating the pyramid together.

We have four triangles that all have the same area and a square that supports the pyramid.

To find the area of the square we take the side length of 15 and square it 

The area of the square is  .

To find the area of the triangle we must use the equation for the area of a triangle which is 

Plug in the slant height 12 as the height of the triangle and use the side length of the square 15 as the base in our equation to get

The area of each triangle is .

We then multiply the area of each triangle by 4 to find the area of all four triangles .

The four triangles have a surface area of .

We add the surface area of the four triangles with the area of the square to get the answer for the surface area of the pyramid which is .

The answer is  .

The formula for the surface area of a pyramid is:

Where  is the length of the slant height,  is the width of the base, and  is the length of the base

In order to determine the areas of the triangle, you will need to use the Pythagorean Theorem to find the slant height:

Plugging in our values, we get:

The formula for the surface area of a pyramid is:

Where  is the length of the base,  is the width of the base, and  is the slant height

Use the Pythagorean Theorem to find the length of the slant height:

Plugging in our values, we get:

The surface area of of a square pyramid can be determined using the following equation:

The surface area of a square pyramid can be broken into the area of the square base and the areas of the four triangluar sides. The area of a square is given by:

The area of a triangle is:

The given height of 12 in is from the vertex to the center of the base. We need to calculate the slant height of the triangular face by using the Pythagorean Theorem: 

where   and   (half the base side) resulting in a slant height of 13 in.

So, the area of the triangle is:

There are four triangular sides totaling  for the sides.

The total surface area is thus , including all four sides and the base.

When reading word problems, there are certain clues that help interpret what is going on. The word “is” generally means “=” and the word “times” means it will be multiplied by something. Therefore, “the length of a box is 3 times the width” gives you the answer: L = 3 x W, or L = 3W.

We notice the width is “5 inches less than three times its width,” so we express W as being three times its width (3L) and 5 inches less than that is 3L minus 5. In this case, W is the dependent and L is the independent variable.

W = 3L - 5