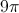We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Geometry

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #7 : How To Find The Volume Of A Cylinder

What is the volume of a cylinder with a circular side with a radius of and a length of ?

Possible Answers:

$84\pi$

$588\pi$

$334\pi$

$168\pi$

Correct answer:

$588\pi$

Explanation:

To find the volume of a cylinder we must know the equation for the volume of a cylinder which is

In this example the length is and the radius is so our equation will look like this $V=(12)(\pi)(7^{2})$

We then square the to get $7^{2}=49$

Then perform multiplication to get $(49)(12)(\pi)=588\pi$

The answer is $588\pi$ .

Report an Error

Example Question #11 : Cylinders

The volume of a cylinder is $54\pi$ units cubed. If the cylinder's height is units, what is its radius?

Possible Answers:

units

Correct answer:

units

Explanation:

The formula for the volume of a cylinder is $V = \pi r^2 \times h$ , where is volume, is the radius of the cylinder, and is its height. Substituing the given information into this equation makes it possible to find the radius by solving for :

$V = \pi r^2 \times h$

$\rightarrow 54\pi = \pi r^2 \times 6$

$\rightarrow \frac{54\pi}{6\pi} = \frac{(\pi r^2 \times 6)}{6\pi}$

$\rightarrow 9 = r^2$

$\rightarrow r = 3$ units

Report an Error

Example Question #651 : Geometry

This figure is a right cylinder with radius of 2 m and a height of 10 m.

What is the volume of the right cylinder (m³)?

Possible Answers:

125.66

150.80

125.71

62.83

25.13

Correct answer:

125.71

Explanation:

The formula for the volume of a right cylinder is $\pi r^{2}h$ where is the radius and is the height. Thus for this problem

$\pi\cdot2^{2}\cdot10=125.71$

Report an Error

Example Question #21 : Cylinders

What is the volume of a cylinder with a radius of and a height of ?

Possible Answers:

$9\pi$

$9\pi+15$

$54\pi$

$135\pi$

$96\pi$

Correct answer:

$135\pi$

Explanation:

When thinking of a 3D figure, think of it as a stack of something. In this case, a cylinder is a stack of a circles.

The volume will be the area of that base circle times the height of the cylinder. Mathematically that would be $V=(\pi r^2)*h$ .

Plug in our given values and solve.

$V=(\pi r^2)*h$

$V=(\pi (3)^2)*15$

$V=9\pi*15$

$V=135\pi$

Report an Error

Example Question #117 : Solid Geometry

Find the volume of a cylinder given that its height and radius are 4 and 11, respectively.

Possible Answers:

$312\pi$

$484\pi$

$225\pi$

$144\pi$

$121\pi$

Correct answer:

$484\pi$

Explanation:

The standard equation to find the volume of a cylinder is

$V=\pi hr^2$

where denotes height and denotes radius.

Plug in the given values for height and radius to find the volume of the cylinder:

$V=\pi \cdot 4(11)^2=4\cdot 121\cdot\pi =484\pi$

Report an Error

Example Question #118 : Solid Geometry

Find the volume of the following cylinder.

Cylinder

Possible Answers:

$545 \pi m^3$

$556 \pi m^3$

$539 \pi m^3$

$530 \pi m^3$

$521 \pi m^3$

Correct answer:

$539 \pi m^3$

Explanation:

The formula for the volume of a cylinder is:

$V = \pi r^2 h$

where is the radius of the base and is the length of the height.

Plugging in our values, we get:

$V = \pi (7m)^2 (11m)$

$V = 539 \pi m^3$

Report an Error

Example Question #1971 : High School Math

Find the volume of the following cylinder.

Cylinder

Possible Answers:

$144 \pi m^3$

$164 \pi m^3$

$154 \pi m^3$

$134 \pi m^3$

$124 \pi m^3$

Correct answer:

$144 \pi m^3$

Explanation:

The formula for the volume of a cylinder is:

V = (base)(height)

$V=(\pi r^2)(h)$

Where is the radius of the base and is the height of the cylinder

Plugging in our values, we get:

$V=\pi (4m)^2(9m)$

$V = 144 \pi m^3$

Report an Error

Example Question #22 : Cylinders

Find the volume of the following partial cylinder.

Cylinder_sector

Possible Answers:

$\frac{160 \pi m^3}{4}$

$\frac{160 \pi m^3}{2}$

$\frac{160 \pi m^3}{6}$

$160 \pi m^3$

$\frac{160 \pi m^3}{3}$

Correct answer:

$\frac{160 \pi m^3}{3}$

Explanation:

The formula for the volume of a partial cylinder is:

V = (base)(height)(part)

$V = (\pi r^2)(h)\left(\frac{part}{360}\right)$

Where is the radius of the cylinder, is the height of the cylinder, and part is the degrees of the sector.

Plugging in our values, we get:

$V = (\pi (8m)^2)(5m)\left(\frac{60}{360}\right)$

$V = \frac{320 \pi m^3}{6}=\frac{160 \pi m^3}{3}$

Report an Error

Example Question #21 : Cylinders

Find the volume of the following partial cylinder.

Partial_cylinder

Possible Answers:

$520 \pi m^3$

$530 \pi m^3$

$540 \pi m^3$

$550 \pi m^3$

$560 \pi m^3$

Correct answer:

$540 \pi m^3$

Explanation:

The formula for the volume of a partial cylinder is:

V = (base)(height)(part)

$V = (\pi r^2)(h)\left(\frac{part}{360}\right)$

where is the radius of the cylinder, is the height of the cylinder, and part is the degrees of the sector.

Plugging in our values, we get:

$V=(\pi (6m)^2)(20m)\left(\frac{270}{360}\right)$

$V=540 \pi m^3$

Report an Error

Example Question #1 : How To Find The Volume Of A Cylinder

If a cylinder has a radius, $\small r$ , of 2 inches and a height, $\small h$ , of 5 inches, what is the total surface area of the cylinder?

Possible Answers:

$\small 18\pi$

$\small 28\pi$

$\small 70\pi$

$\small 36\pi$

$\small 24\pi$

Correct answer:

$\small 28\pi$

Explanation:

The total surface area will be equal to the area of the two bases added to the area of the outer surface of the cylinder. If "unwrapped" the area of the outer surface is simply a rectangle with the height of the cylinder and a base equal to the circumference of the cylinder base. We can use these relationships to find a formula for the total area of the cylinder.

$A=2A_{base}+A_{rectangle}$

$A=2(\pi r^2)+(2\pi r)(h)$

Use the given radius and height to solve for the final area.

$\small 2\pi(2)^{2} + 2\pi (2)(5)$

$\small 8\pi + 20\pi$

$\small 28\pi$

Report an Error

View Tutors

Toniann
Certified Tutor

Florida International University, Masters in Education, Curriculum and Instruction.

View Tutors

Krystal
Certified Tutor

Ohio State University-Main Campus, Bachelor of Education, Education. University of Dayton, Masters in Education, Education.

View Tutors

Joanna
Certified Tutor

Texas Christian University, Bachelor of Education, English.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

English Tutors in Miami, GMAT Tutors in Boston, GMAT Tutors in New York City, ISEE Tutors in Seattle, GMAT Tutors in Chicago, ISEE Tutors in Denver, Spanish Tutors in Boston, French Tutors in New York City, MCAT Tutors in Atlanta, Math Tutors in New York City

Popular Courses & Classes

SSAT Courses & Classes in Chicago, ACT Courses & Classes in Denver, SSAT Courses & Classes in New York City, ISEE Courses & Classes in San Diego, MCAT Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Chicago, ACT Courses & Classes in Houston, GMAT Courses & Classes in Phoenix, MCAT Courses & Classes in New York City, MCAT Courses & Classes in Chicago

Popular Test Prep

GMAT Test Prep in Phoenix, LSAT Test Prep in Seattle, MCAT Test Prep in Denver, SSAT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Washington DC, GMAT Test Prep in San Diego, ACT Test Prep in Denver, GMAT Test Prep in Philadelphia, SSAT Test Prep in Miami, SAT Test Prep in Los Angeles

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Geometry

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #7 : How To Find The Volume Of A Cylinder

Example Question #11 : Cylinders

Example Question #651 : Geometry

Example Question #21 : Cylinders

Example Question #117 : Solid Geometry

Example Question #118 : Solid Geometry

Example Question #1971 : High School Math

Example Question #22 : Cylinders

Example Question #21 : Cylinders

Example Question #1 : How To Find The Volume Of A Cylinder

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: