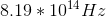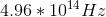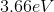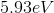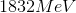The net work is equal to the pressure times the change in volume. So the pressure is  and the change in volume is . Multiplying the two will equal .

We're asked to find the amount of heat energy that must be added to a balloon undergoing expansion against a constant external pressure in order for it to maintain a constant temperature.

The situation being described in the question stem is one of isothermal expansion, meaning that the temperature doesn't change. In other words, we can say that the internal energy of the gas held within the balloon does not change.

Furthermore, we can define the amount of work done by the gas on the balloon as follows.

Combining these expression, we can obtain the following.

Finally, if we plug in the values given to us, we can get our answer.

Using

Converting to and plugging in values

Using

is the photon energy

is Plank's constant,

is the speed of light,

is the wavelength

Converting to and plugging in values:

The wavelength of the light beam doesn't depend on the speed through the medium. As such, as can solve for wavelength  by simply solving:

Where  is frequency and  is the speed of light in a vacuum. 

To determine the work function of the metal, we can begin by calculating the kinetic energy of the electron from its speed.

Then, convert joules into electron volts:

Next, we'll calculate the energy of the light by using its frequency according to the equation:

Then, we can convert this energy into electron volts:

And finally, we can use the equation for work function:

The energy difference between the second excited state  and the ground state  will be equal to the photon energy since energy is conserved.

Since the energy difference is in electron volts, they need to be converted to Joules. Another convenient formula is to notice that since  and  are constants, they can be converted to electron volts and you can use

The ejection of electrons from a metal is known as the photoelectric effect. In fact, it was a key discovery that led to the acceptance of the particle nature of light, because the wave nature of light could not account for this finding.

The key that allowed scientists to find this out was that the speed of electrons ejected from the metal was dependent on the color of the light. The intensity of light had no effect on the speed at which electrons were ejected.

As a part of developing this theory, scientists referred to individual discrete particles of light as photons. In order to eject electrons from the metal, individual photons needed to have a sufficient amount of energy. The intensity of light (with a greater amplitude of its waves) represents a case in which photons are striking the metal at a greater rate. But, the individual energy of the photons could be too low in such a situation, hence why intensity is not the key property here. Instead, a higher frequency of light allows each individual photon to have greater energy - enough to knock the metal's electrons off. Furthermore, as the frequency of the light increases, the energy of the individual photons increases and the kinetic energy of the ejected electrons increases as well. The expression for the energy of a photon is shown as follows.

This is an example of one of Einstein's greatest ideas: the relation between the mass of an object/particle, and the energy contained by the mass. This is given as

In order to calculate the energy in our particle, we must make sure that the mass is in units of .

Now we can plug in numbers to our equation and solve for energy.

In this question, we're presented with information concerning the mass of a uranium atom. We're told two values: the mass of a uranium atom as measured, and the predicted mass of a uranium atom. We're then asked to determine the nuclear binding energy for uranium.

In order to solve this question, we have to realize the significance of the discrepancy between the observed and predicted mass of uranium. The predicted mass is calculated by adding up the individual masses of each constituent proton, electron, and neutron. However, the reason why the measured mass is less than the predicted mass is due to energy-mass equivalence. When the constituent protons and neutrons come together to form the nucleus, some of their mass is converted into energy, and it is this energy which holds these constituent nucleons together. Because some of the mass is converted into energy, the observed mass is less than what we would predict.

Now that we understand why there is a discrepancy between observed and predicted mass, we can calculate the nuclear binding energy by using Einstein's famous equation.

This equation states that the nuclear binding energy is equal to the difference between observed and predicted mass, multiplied by the speed of light squared. So to solve for energy, we can plug in the values given to us.