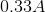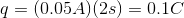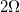
Recall that the current through resistors connected in series is the equal for all components. The current through the first resistor and the current through the second resistor should be the same.

The first step in solving involves calculating the equivalent resistance of the circuit. Since the resistors are in series the equivalent resistance of this circuit is the sum of the two resistances.

Now we can use Ohm’s law to solve for the current.

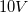
To solve this question you need to use the Ohm’s law and the definition of an electric current. Ohm’s law states that voltage is the product of current and resistance:

The definition of electric current is given by the charge per unit time:

Using these equations it is possible to solve for the charge. The trick is to first solve for the current using Ohm’s law and the given voltage and resistance.

Now that we know the current and the time, we can solve for the charge using our second equation.

The standard unit for power is Watts, but other equivalent units can be derived from the equations for power.

Remember that power is defined as work per unit time:

The units from this equation will be Joules per second, eliminating that answer choice.

In terms of circuits, power is defined as the product of current and voltage, giving the units Ampere-Volts:

If you combine Ohm’s law and the definition of power you can rewrite the equation for power as follows:

These units will be Amperes squared times Ohms.

The only answer choice you are left with is Ohm-Volts. Power in terms of resistance and voltage is:

Since the resistors are connected in series, they will have the same current flowing through them. In series current is constant across resistors, and in parallel voltage is constant across resistors.

Remember the equations for voltage and power. The equation for voltage is Ohm's law:

Power can be written in terms of voltage and resistance, but in this problem only the current is held constant (because the resistors are in series) while the voltage of the resistors is different. The appropriate equation to use for comparison is:

From the equations you can deduce that increasing resistance will increase both voltage and power. The best answer is that current through both resistors is the same, but the larger resistor will have higher voltage and power dissipation.

According to Ohm’s law a decrease in current and/or resistance will lead to a decrease in voltage, since voltage is directly proportional to both current and resistance.

Increasing the current will not decrease voltage. Remember that resistance is defined as:

In this formula, is the resistivity, is the length of the wire, and  is the cross-sectional area of the wire. Increasing length will lead to an increase in resistance and voltage; however, increasing the area will lead to a decrease in resistance and, subsequently, a decrease in voltage.

The only answer that will lead to a decrease in voltage is the choice to increase the cross-sectional area of the wire.

Replacing the copper wire with a more conductive material will increase the resistivity, which will subsequently increase resistance and voltage.

When circuit elements, such as resistors, are connected in parallel they will have the same voltage drop. The current through the resistor will be greater than current through the resistor, but their voltages will be equal. According to Ohm’s law the current flowing through the smaller resistor will be larger. Ohm’s law can be rearranged to solve for current as follows:

Since voltage is the same across resistors, the lower resistance () will have more current flowing through it since current is inversely proportional to resistance.

The student's hand on the sphere "grounds" it, allowing charges to flow in or out. No charge flows through the styrofoam insulator. When the negatively charged rod is brought nearby, negative charges in the sphere are repelled and exit via the student's hand, giving the sphere a net positive charge. After the student removes his hand, no more charges can flow into or out from the sphere, so the net positive charge remains after the rod is removed. Since this is a conducting sphere, the charges will spread out evenly over the surface.

We are asked how much charge is stored in total on the circuit. We can use the equivalent capacitance and the voltage supplied by the battery to calculate the charge. Remember that Q = CV, where Q is the total charge, C is the equivalent capacitance, and V is the voltage. We must first solve for equivalent capacitance.

C₂ and C₃ are capacitors in series, while C₁ is in parallel.

C₂₃ = 0.5μF

C_eq = C₂₃ + C₁ = 0.5μF + 0.5μF = 1μF

Now we can plug in the C_eq and battery voltage to find the charge.

Q = (1μF)(10V) = 10μC

Given Coulomb's Law electrostatic forces:

We can see that distance and force are inversly related. Also distance is squared, so if we increase the distance by 2, the force between the two charges will be reduced by a factor of four.

For this problem we must understand Coulomb's Law. The force on charge A will be dircetly affected by the charge of Q1 and Q2. Q1 and Q2 are both negative, they will both attract charge A, and the net force will be reduced as they pull in opposite directions. Switching Q2 to a positive charge will result in a repulsive force on charge A which will be in the same direction as the attractive force between Q1 and A.