All AP Physics 2 Resources
Example Questions
Example Question #4 : Other Principles Of Quantum Mechanics
The square modulus of the wavefunction, given as 






By definition, 
Example Question #1 : Atomic And Nuclear Physics
What is the speed of an electron in the first Bohr orbit in meters per second?
To find the speed of the electron, use the following formula:
Substitute all the knowns and solve for velocity.
Example Question #2 : Atomic And Nuclear Physics
Suppose that an electron within a hydrogen atom moves from the fourth energy level to the second energy level. What is the wavelength of the photon emitted during this process?
To answer this question, we'll need to utilize the equation that specifies the energy level of electrons within a hydrogen atom.
Where 

The negative sign for the change in energy just means that energy is being released in this process. We can drop the negative because we know that energy is being released.
Now that we've found how much energy is contained in the released photon, we'll need to calculate its wavelength.
Example Question #1 : Atomic And Nuclear Physics
An electron collides with an atom, exciting an electron in the atom from it's ground state 


The incoming electron will lose kinetic energy during the collision, transfering this energy to the potential energy of the bound electron in the atom. Conservation of energy can be used to solve this problem. The general statement that energy is conserved is
where 


The incoming electron will still have kinetic energy after the collision but the bound electron will not since it is not a free electron. This means that
where
plugging this in -


Example Question #4 : Atomic And Nuclear Physics
Calculate the energy released as a photon when an electron falls from the 

During a energy level change in a hydrogen atom, the amount of energy either lost of gained is given by the following equation with respect to the initial and final energy levels shown below.
Recall that whenever electrons drop from higher energy levels to lower ones, energy can be released in the form of a photon. To obtain the amount of energy released, we mst take the difference in energy of the electrons at the particular energy levels:
It is important to note that the negative energy difference corresponds to how much energy the photon is "taking away" as it leaves. Therefore, the photon leaves the atom with 
Example Question #5 : Atomic And Nuclear Physics
An electron in a hydrogen atom falls from the 

None of these
Using
Plugging in values:
This will be the change in energy of the electron, which is the negative of the energy of the photon released.
Thus, the energy of the photon is
Example Question #1 : Electron Energy Levels
How much energy would it take to raise an electron from the 

None of these
Using the formula for the energy of an electron in a hydrogen atom's nth energy level:
Plug in 

Convert electronvolts to Joules:
Example Question #7 : Atomic And Nuclear Physics
One mole of hydrogen atoms have electrons drop from the 

None of these
Using the following equation for the energy of an electron in Joules:
And
Combining equations and plugging in values:

Example Question #8 : Atomic And Nuclear Physics
What is the difference in energy for a hydrogen atom with its electron in the ground state and a hydrogen atom with its electron in the 
For this question, we need to compare the difference in energy levels of hydrogen atoms with electrons in different orbitals.
First, we will need to use the equation that describes the energy of an electron in a hydrogen atom.
In the above expression, 
First, let's see what the electron energy level is in the ground state, which corresponds to 
Next, let's do the same thing for the 
Next, we can find the difference in the energy values.
Example Question #9 : Atomic And Nuclear Physics
By what process is 


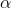

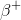
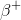
To answer this question, we'll need to consult the periodic table. From the table, we know that magnesium's atomic number (the number of protons it contains in its nucleus) is 12, and sodium's is 11. We also need to realize that the mass number for each (the number of protons plus neutrons contained in the nucleus) is the same. Since the mass numbers are the same but the atomic numbers differ by one, then we can infer that a neutron is undergoing a decay into a proton and a so called positron, 
Furthermore, it cannot be alpha decay, because in this process an alpha nucleus is released and the reactant's mass number and atomic number would both change. It also cannot be gamma decay, because in this process there is no change in atomic or mass numbers. Finally, it cannot be electron capture because in this process, an electron combines with a proton to generate a neutron. Thus, the mass number would not change, but the atomic number would increase by one. But in the question stem, we know the atomic number is decreasing by one rather than increasing.
All AP Physics 2 Resources






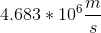






















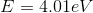






![U_{f}=\frac{1}{2}m \left ( v_{f}\right )^{2}-\frac{1}{2}m \left ( v_{i}\right )^{2}=\frac{1}{2}m \left [ \left ( v_{f}\right )^{2}-\left ( v_{i}\right )^{2} \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/550201/gif.latex)















































