All SSAT Upper Level Math Resources
Example Questions
Example Question #131 : Grade 8
Find the y-intercept:
Rewrite the equation in slope-intercept form, .
The y-intercept is , which is .
Example Question #501 : Ssat Upper Level Quantitative (Math)
What is the -intercept of the graph of the function
The graph has no -intercept.
The -intercept of the graph of a function is the point at which it intersects the -axis - that is, at which . This point is , so evaluate :
The -intercept is .
Example Question #12 : How To Find X Or Y Intercept
Define a function . Which of the following is the -intercept of the graph of ?
The -intercept of the graph of a function has 0 as its -coordinate, since it is defined to be the point at which it crosses the -axis. Its -coordinate is , which can be found using substitution, as follows:
The correct choice is .
Example Question #13 : How To Find X Or Y Intercept
Define a function . Which of the following is an -intercept of the graph of ?
(a)
(b)
Both (a) and (b)
(a), but not (b)
(b), but not (a)
Neither (a) nor (b)
Neither (a) nor (b)
An -intercept of the graph of a function has 0 as its -coordinate, since it is defined to be a point at which it crosses the -axis. Its -coordinate is a value of for which .
We can most easily determine whether is a point on the graph of by proving or disproving that , which we can do by substituting 2 for :
, so is not an -intercept.
Similarly, substituting 3 for :
, so is not an -intercept.
Example Question #15 : How To Find X Or Y Intercept
Define . The graphs of and a second function, , intersect at their common -intercept. Which of the following could be the definition of ?
An -intercept of the graph of a function has 0 as its -coordinate, since it is defined to be a point at which it crosses the -axis. Its -coordinate is a value of for which , which can be found as follows:
Substituting the definition, we get
Solving for by subtracting 7 from both sides, then dividing both sides by 2:
The -intercept of the graph of is the point .
To determine which of the four choices is correct, substitute for and determine for which definition of it holds that .
can be eliminated immediately as a choice since it cannot take the value 0.
:
The correct choice is .
Example Question #1 : How To Find The Equation Of A Curve
If the -intercept of the line is and the slope is , which of the following equations best satisfies this condition?
Write the slope-intercept form.
The point given the x-intercept of 6 is .
Substitute the point and the slope into the equation and solve for the y-intercept.
Substitute the y-intercept back to the slope-intercept form to get your equation.
Example Question #2 : How To Find The Equation Of A Curve
A vertical parabola on the coordinate plane has vertex and -intercept .
Give its equation.
Insufficient information is given to determine the equation.
The equation of a vertical parabola, in vertex form, is
,
where is the vertex. Set :
To find , use the -intercept, setting :
The equation, in vertex form, is ; in standard form:
Example Question #3 : How To Find The Equation Of A Curve
A vertical parabola on the coordinate plane has vertex ; one of its -intercepts is .
Give its equation.
Insufficient information is given to determine the equation.
The equation of a vertical parabola, in vertex form, is
,
where is the vertex. Set :
To find , use the known -intercept, setting :
The equation, in vertex form, is ; in standard form:
Example Question #231 : Coordinate Geometry
A vertical parabola on the coordinate plane has -intercept ; its only -intercept is .
Give its equation.
Insufficient information is given to determine the equation.
If a vertical parabola has only one -intercept, which here is , that point doubles as its vertex as well.
The equation of a vertical parabola, in vertex form, is
,
where is the vertex. Set :
To find , use the -intercept, setting :
The equation, in vertex form, is . In standard form:
Example Question #5 : How To Find The Equation Of A Curve
A vertical parabola on the coordinate plane has -intercept ; one of its -intercepts is .
Give its equation.
Insufficient information is given to determine the equation.
Insufficient information is given to determine the equation.
The equation of a vertical parabola, in standard form, is
for some real .
is the -coordinate of the -intercept, so , and the equation is
Set :
However, no other information is given, so the values of and cannot be determined for certain. The correct response is that insufficient information is given.
Certified Tutor
All SSAT Upper Level Math Resources
















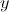

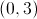
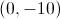















































































































![y = a[x-(-4)]^{2}+10](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/349648/gif.latex)
























![y = a[x-(-3)]^{2}+ (-6)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/349578/gif.latex)































































