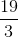We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : SSAT Upper Level Quantitative (Math)

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #252 : Geometry

Find the slope of a line that passes through the points (17,2) and (-2, -1) .

Possible Answers:

$-\frac{19}{3}$

$\frac{3}{19}$

$\frac{19}{3}$

$-\frac{3}{19}$

Correct answer:

$\frac{3}{19}$

Explanation:

To find the slope of the line that passes through the given points, you can use the slope equation.

$\text{Slope}=\frac{y_2-y_1}{x_2-x_1}$

$\text{Slope}=\frac{-1-2}{-2-17}=\frac{-3}{-19}=\frac{3}{19}$

Report an Error

Example Question #253 : Geometry

Find the slope of the line that passes through the points (a, b) and (2, 3) .

Possible Answers:

$\frac{3-b}{2-a}$

$\frac{2-a}{3-b}$

$\frac{2-b}{3-a}$

$\frac{3-a}{2-b}$

Correct answer:

$\frac{3-b}{2-a}$

Explanation:

To find the slope of the line that passes through the given points, you can use the slope equation.

$\text{Slope}=\frac{y_2-y_1}{x_2-x_1}$

$\text{Slope}=\frac{3-b}{2-a}$

Report an Error

Example Question #251 : Geometry

A line has the equation 5x-9y=12 . What is the slope of this line?

Possible Answers:

$\frac{9}{5}$

$\frac{5}{9}$

$-\frac{4}{3}$

Correct answer:

$\frac{5}{9}$

Explanation:

You need to put the equation in y=mx+b form before you can easily find out its slope.

5x-9y=12

-9y=-5x+12

$y=\frac{5}{9}x-\frac{4}{3}$

Since $m=\frac{5}{9}$ , that must be the slope.

Report an Error

Example Question #201 : Coordinate Geometry

Find the slope of the line that goes through the points (4t, 8s) and (2t, -9s) .

Possible Answers:

$\frac{6t}{-s}$

$\frac{17s}{2t}$

$\frac{-s}{6t}$

$\frac{2t}{17s}$

Correct answer:

$\frac{17s}{2t}$

Explanation:

Even though there are variables involved in the coordinates of these points, you can still use the slope formula to figure out the slope of the line that connects them.

$\text{Slope}=\frac{y_2-y_1}{x_2-x_1}$

$\text{Slope}=\frac{-9s-8s}{2t-4t}=\frac{-17s}{-2t}=\frac{17s}{2t}$

Report an Error

Example Question #2 : Use Similar Triangles To Show Equal Slopes: Ccss.Math.Content.8.Ee.B.6

The equation of a line is 12x-8y=6 . Find the slope of this line.

Possible Answers:

$-\frac{3}{2}$

$\frac{3}{2}$

$\frac{3}{4}$

$-\frac{3}{4}$

Correct answer:

$\frac{3}{2}$

Explanation:

To find the slope, you will need to put the equation in y=mx+b form. The value of will be the slope.

12x-8y=6

Subtract from either side:

8y=12x-6

Divide each side by :

$y=\frac{3}{2}x-\frac{3}{4}$

You can now easily identify the value of .

$m=\frac{3}{2}$

Report an Error

Example Question #202 : Coordinate Geometry

Find the slope of the line that passes through the points (0,3) and (8,1) .

Possible Answers:

$\frac{1}{4}$

$-\frac{1}{4}$

Correct answer:

$-\frac{1}{4}$

Explanation:

You can use the slope formula to figure out the slope of the line that connects these two points. Just substitute the specified coordinates into the equation and then subtract:

$\text{Slope}=\frac{y_2-y_1}{x_2-x_1}$

$\text{Slope}=\frac{3-1}{0-8}=\frac{2}{-8}=-\frac{1}{4}$

Report an Error

Example Question #263 : Geometry

Find the slope of the following function: 2x-6y=3

Possible Answers:

$\frac{1}{3}$

Correct answer:

$\frac{1}{3}$

Explanation:

Rewrite the equation in slope-intercept form, y=mx+b .

2x-6y=3

2x=3+6y

2x-3=6y

$\frac{2x-3}{6}=y$

$y=\frac{1}{3}x-\frac{1}{2}$

The slope is the term, which is $\frac{1}{3}$ .

Report an Error

Example Question #264 : Geometry

Find the slope of the line given the two points: $(5,8) \textup{ and } (-3,-7)$

Possible Answers:

$\frac{15}{8}$

$-\frac{15}{8}$

$\frac{8}{15}$

$-\frac{8}{15}$

$\frac{4}{3}$

Correct answer:

$\frac{15}{8}$

Explanation:

Write the formula to find the slope.

$m=\frac{y_2-y_1}{x_2-x_1}=\frac{y_1-y_2}{x_1-x_2}$

Either equation will work. Let's choose the latter. Substitute the points.

$m=\frac{y_1-y_2}{x_1-x_2}=\frac{8-(-7)}{5-(-3)}= \frac{15}{8}$

Report an Error

Example Question #4 : Slope

What is the slope of the line with the equation 2x+3y=-9?

Possible Answers:

$-\frac{3}{2}$

$-\frac{2}{3}$

Correct answer:

$-\frac{2}{3}$

Explanation:

To find the slope, put the equation in the form of y=mx+b .

2x+3y=-9

3y=-2x-9

$y=-\frac{2}{3}x-3$

Since $m=-\frac{2}{3}$ , that is the value of the slope.

Report an Error

Example Question #11 : How To Find Slope

Consider the line of the equation f(x) = 5x - 17 . The line of a function g(x) has the same slope as that of f(x) . Which of the following could be the definition of g(x) ?

Possible Answers:

g(x) =10x - 34

g (x) = 5x - 34

g(x) = 10 x - 17

g(x) = 17x - 5

Correct answer:

g (x) = 5x - 34

Explanation:

The definition of f(x) is written in slope-intercept form f(x )= mx + b , in which , the coefficient of , is the slope of its line. f(x) = 5x - 17 , so the slope of its line is m = 5 .

We must select the choice whose line has this slope. The definition of g(x) in each choice is also written in slope-intercept form, so we select the alternative with -coefficient 5; the only such alternative is g (x) = 5x - 34 .

Report an Error

View SSAT- Upper Level Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

View SSAT- Upper Level Tutors

Joseph
Certified Tutor

CUNY College of Staten Island, Bachelor in Arts, Applied Psychology. New York University, Master of Arts, Applied Psychology.

View SSAT- Upper Level Tutors

Keith
Certified Tutor

Xavier University, Bachelor in Business Administration, Accounting. Ohio University-Main Campus, Masters in Education, Mathem...

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Physics Tutors in Philadelphia, Reading Tutors in Philadelphia, GMAT Tutors in Boston, Statistics Tutors in Atlanta, Algebra Tutors in Dallas Fort Worth, SAT Tutors in Denver, SAT Tutors in San Francisco-Bay Area, GRE Tutors in Denver, SSAT Tutors in Washington DC, Statistics Tutors in Miami

Popular Courses & Classes

SSAT Courses & Classes in Houston, MCAT Courses & Classes in Boston, MCAT Courses & Classes in Philadelphia, ISEE Courses & Classes in Philadelphia, LSAT Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in Denver, GMAT Courses & Classes in Denver, ACT Courses & Classes in Dallas Fort Worth, ACT Courses & Classes in Los Angeles, SSAT Courses & Classes in Phoenix

Popular Test Prep

MCAT Test Prep in Philadelphia, LSAT Test Prep in Dallas Fort Worth, MCAT Test Prep in San Diego, GRE Test Prep in Houston, ACT Test Prep in Phoenix, GRE Test Prep in Boston, GRE Test Prep in San Diego, MCAT Test Prep in Houston, SAT Test Prep in San Francisco-Bay Area, GRE Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : SSAT Upper Level Quantitative (Math)

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #252 : Geometry

Example Question #253 : Geometry

Example Question #251 : Geometry

Example Question #201 : Coordinate Geometry

Example Question #2 : Use Similar Triangles To Show Equal Slopes: Ccss.Math.Content.8.Ee.B.6

Example Question #202 : Coordinate Geometry

Example Question #263 : Geometry

Example Question #264 : Geometry

Example Question #4 : Slope

Example Question #11 : How To Find Slope

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: