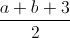We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : SSAT Upper Level Quantitative (Math)

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #112 : Coordinate Geometry

Give the length, in terms of , of a segment on the coordinate plane whose endpoints are (A+2, A-2) and the origin.

Possible Answers:

$\sqrt{ 2A^{2}- 8 }$

$2 \sqrt{2A}$

$\sqrt{ 2A^{2}+ 8A+8 }$

$\sqrt{ 2A^{2}+ 8 }$

$\sqrt{ 2A^{2}- 8A+8 }$

Correct answer:

$\sqrt{ 2A^{2}+ 8 }$

Explanation:

The distance between two points $(x_{1}, x_{2})$ and $(y_{1}, y_{2})$ can be obtained using the formula

$d = \sqrt{\left (x_{2}-x_{1} \right )^{2}+\left (y_{2}-y_{1} \right )^{2}}$

Setting $x_{1}= y_{1} = 0, x_{2}=A+2, y_{2} = A-2$ , we can find our expression:

$d = \sqrt{\left ( \left [A+2 \right )-0\right ]^{2}+\left [\left (A-2 \right )-0 \right ] ^{2}}$ $= \sqrt{\left ( A+2 \right ) ^{2}+ \left (A-2 \right ) ^{2}}$

$= \sqrt{\left ( A^{2}+4A+4 \right )+\left ( A^{2}-4A+4 \right ) }$

$= \sqrt{ 2A^{2}+ 8 }$

Report an Error

Example Question #113 : Coordinate Geometry

Give the length, in terms of , of a segment on the coordinate plane whose endpoints are (A,A) and (3,3)

Possible Answers:

A - 3

$\sqrt{2A^{2}-12A+18 }$

$\sqrt{2A^{2} -18 }$

$\sqrt{2A^{2} +18 }$

$\sqrt{2A^{2}+12A+18 }$

Correct answer:

$\sqrt{2A^{2}-12A+18 }$

Explanation:

The distance between two points $(x_{1}, x_{2})$ and $(y_{1}, y_{2})$ can be obtained using the formula

$d = \sqrt{\left (x_{2}-x_{1} \right )^{2}+\left (y_{2}-y_{1} \right )^{2}}$

Setting $x_{1}= y_{1} =3, x_{2}= y_{2} = A$ , we can find our expression:

$d = \sqrt{\left (A-3 \right )^{2}+\left (A-3\right )^{2}}$

$= \sqrt{\left (A^{2}-6A+9 \right ) + \left (A^{2}-6A+9 \right ) }$

$= \sqrt{2A^{2}-12A+18 }$

Report an Error

Example Question #161 : Geometry

A line segment on the coordinate plane has endpoints (a-5,-b) and (b+8, a-4) . In terms of and , as applicable, give the -coordinate of its midpoint.

Possible Answers:

$\frac{a - b - 4}{2}$

$\frac{a - b - 13}{2}$

$\frac{a + b + 3}{2}$

a - b - 4

a + b + 3

Correct answer:

$\frac{a + b + 3}{2}$

Explanation:

The -coordinate of the midpoint of a line segment is the mean of the -coordinates of its endpoints. Therefore, the -coordinate is

$x= \frac{(a-5)+(b+8)}{2} = \frac{a+b-5+8}{2} = \frac{a+b+3}{2}$ .

Report an Error

Example Question #391 : Ssat Upper Level Quantitative (Math)

A line segment on the coordinate plane has endpoints (a-5,-b) and (b+8, a-4) . In terms of and , as applicable, give the -coordinate of its midpoint.

Possible Answers:

$\frac{a - b - 4}{2}$

$\frac{a + b - 4}{2}$

a + b + 3

a - b - 4

$\frac{a + b + 3}{2}$

Correct answer:

$\frac{a - b - 4}{2}$

Explanation:

The -coordinate of the midpoint of a line segment is the mean of the -coordinates of its endpoints. Therefore, the -coordinate is

$y= \frac{(a-4)+(-b)}{2} = \frac{a-b-4}{2}$ .

Report an Error

Example Question #172 : Geometry

A line segment has the endpoints (6,10) and (-2, -4) . What is the midpoint of the line?

Possible Answers:

(2, 3)

(4,6)

(4,7)

(8,14)

Correct answer:

(2, 3)

Explanation:

To find the midpoint of a line, take the averages of the x-coordinates and the average of the y-coordinates.

$\text{Midpoint}=(\frac{6+(-2)}{2}, \frac{10+(-4)}{2})=(\frac{4}{2}, \frac{6}{2})=(2,3)$

Report an Error

Example Question #2 : Midpoint Formula

What is the midpoint of a line segment with endpoints (12,2) and (-2, 1) ?

Possible Answers:

$(\frac{13}{2}, 0)$

(10, 3)

(14,1)

$(5, \frac{3}{2})$

Correct answer:

$(5, \frac{3}{2})$

Explanation:

To find the midpoint of a line, just take the average of the -coordinates and the average of the -coordinates.

$\text{Midpoint}=(\frac{12+(-2)}{2}, \frac{2+1}{2})=(\frac{10}{2}, \frac{3}{2})=(5, \frac{3}{2})$

Report an Error

Example Question #173 : Geometry

What is the midpoint of a line segments with endpoints (2a, -b) and (4a, 5b) ?

Possible Answers:

(3a, 2b)

(3, 4)

(-a, -2b)

(6a, 4b)

Correct answer:

(3a, 2b)

Explanation:

To find the midpoint of a line segment, take the average of the -coordinates, then take the average of the -coordinates.

$\text{Midpoint}=(\frac{2a+4a}{2}, \frac{-b+5b}{2})$

$\text{Midpoint}=(\frac{6a}{2}, \frac{4b}{2})=(3a, 2b)$

Report an Error

Example Question #174 : Geometry

A line has the endpoints $(8,8) \text{ and }(2, -1)$ . What is its midpoint?

Possible Answers:

(5, 7)

(10, 7)

$\left(5, \frac{7}{2}\right)$

$\left(\frac{7}{2}, 5\right)$

Correct answer:

$\left(5, \frac{7}{2}\right)$

Explanation:

The coordinates of the midpoint of a line are just the averages of the coordinates of the endpoints.

$\text{Midpoint}=\left(\frac{8+2}{2}, \frac{8-1}{2}\right)=\left(5, \frac{7}{2}\right)$

Report an Error

Example Question #175 : Geometry

A line segment has endpoints $(-2, 0) \text{ and }(1, 5)$ . What is the midpoint of this line segment?

Possible Answers:

$\left(-\frac{1}{2}, \frac{5}{2}\right)$

$\left(5, -\frac{1}{2}\right)$

$\left(-\frac{1}{2}, 5\right)$

(-1, 5)

Correct answer:

$\left(-\frac{1}{2}, \frac{5}{2}\right)$

Explanation:

To find the coordinates of the midpoint of a line, take the averages of the x and y coordinates of the endpoints.

$\text{Midpoint}=\left(\frac{-2+1}{2}, \frac{5+0}{2}\right)=\left(-\frac{1}{2}, \frac{5}{2}\right)$

Report an Error

Example Question #8 : How To Find The Midpoint Of A Line Segment

What is the midpoint of a line if the endpoints of the line are: $(6,9) \textup{ and }(3,-2)$ ?

Possible Answers:

$\left(-\frac{3}{2},\frac{1}{2}\right)$

$\left(-\frac{3}{2},-\frac{11}{2}\right)$

$\left(\frac{9}{2},\frac{7}{2}\right)$

$\left(\frac{7}{2},\frac{9}{2}\right)$

$\left(\frac{3}{2},\frac{11}{2}\right)$

Correct answer:

$\left(\frac{9}{2},\frac{7}{2}\right)$

Explanation:

Write the midpoint formula.

$M=\left(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}\right)$

Substitute the values.

$M=\left(\frac{6+3}{2},\frac{9-2}{2}\right)= \left(\frac{9}{2},\frac{7}{2}\right)$

Report an Error

View SSAT- Upper Level Tutors

Crystal
Certified Tutor

SUNY at Binghamton, Bachelor of Science, Mechanical Engineering.

View SSAT- Upper Level Tutors

Keith
Certified Tutor

Xavier University, Bachelor in Business Administration, Accounting. Ohio University-Main Campus, Masters in Education, Mathem...

View SSAT- Upper Level Tutors

Carneta
Certified Tutor

Langston University, Bachelor in Arts, Theater Arts.

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

English Tutors in New York City, Statistics Tutors in Washington DC, GRE Tutors in Atlanta, Math Tutors in Houston, ISEE Tutors in Dallas Fort Worth, MCAT Tutors in Dallas Fort Worth, Reading Tutors in Phoenix, Biology Tutors in Miami, Computer Science Tutors in Dallas Fort Worth, SSAT Tutors in Phoenix

Popular Courses & Classes

ISEE Courses & Classes in San Diego, GMAT Courses & Classes in Houston, Spanish Courses & Classes in Seattle, GMAT Courses & Classes in Atlanta, Spanish Courses & Classes in Phoenix, GRE Courses & Classes in Boston, ISEE Courses & Classes in Miami, GMAT Courses & Classes in Washington DC, GMAT Courses & Classes in Denver, GRE Courses & Classes in San Diego

Popular Test Prep

LSAT Test Prep in San Francisco-Bay Area, ISEE Test Prep in San Diego, LSAT Test Prep in New York City, SSAT Test Prep in Miami, SAT Test Prep in Phoenix, MCAT Test Prep in Miami, GRE Test Prep in San Diego, SAT Test Prep in Houston, GMAT Test Prep in Chicago, GRE Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : SSAT Upper Level Quantitative (Math)

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #112 : Coordinate Geometry

Example Question #113 : Coordinate Geometry

Example Question #161 : Geometry

Example Question #391 : Ssat Upper Level Quantitative (Math)

Example Question #172 : Geometry

Example Question #2 : Midpoint Formula

Example Question #173 : Geometry

Example Question #174 : Geometry

Example Question #175 : Geometry

Example Question #8 : How To Find The Midpoint Of A Line Segment

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: