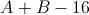Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : SSAT Upper Level Quantitative (Math)

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Endpoints Of A Line Segment

A line segment on the coordinate plane has midpoint $\left ( A + 5, B + 7\right )$ . One of its endpoints is $\left ( 10, 6 \right )$ . What is the -coordinate of the other endpoint, in terms of and/or ?

Possible Answers:

2B + 1

2B + 8

2B + 20

B + 8

B + 1

Correct answer:

2B + 8

Explanation:

Let be the -coordinate of the other endpoint. Since the -coordinate of the midpoint of the segment is the mean of those of the endpoints, we can set up an equation as follows:

$\frac{Y + 6 }{2} = B + 7$

$\frac{Y + 6 }{2} \cdot 2= \left ( B + 7 \right )\cdot 2$

Y + 6 = 2B + 14

Y + 6 -6 = 2B + 14 -6

Y = 2B + 8

Report an Error

Example Question #171 : Geometry

A line segment on the coordinate plane has one endpoint at $\left ( 8, 10 \right )$ ; its midpoint is $\left ( A+B, A- B\right )$ . Which of the following gives the -coordinate of its other endpoint in terms of and ?

Possible Answers:

2 A + 2B- 8

A + B- 8

A + B- 16

A + B+8

2 A + 2B+8

Correct answer:

2 A + 2B- 8

Explanation:

To find the value of the -coordinate of the other endpoint, we will assign the variable . Then, since the -coordinate of the midpoint of the segment is the mean of those of its endpoints, the equation that we can set up is

$\frac{T + 8 }{2} = A + B$ .

We solve for :

$\frac{T + 8 }{2} \cdot 2 =\left ( A + B \right )\cdot 2$

T + 8 =2 A + 2B

T + 8 - 8 =2 A + 2B- 8

T =2 A + 2B- 8

Report an Error

Example Question #121 : Coordinate Geometry

One endpoint of a line segment on the coordinate plane is the point $\left (2\frac{4}{5}, -1\frac{1}{5} \right )$ ; the midpoint of the segment is the point $\left (6\frac{1}{2}, 4\frac{1}{2} \right )$ . Give the -coordinate of the other endpoint of the segment.

Possible Answers:

$10\frac{1}{5}$

$4 \frac{3}{20}$

$-5\frac{1}{5}$

$9\frac{3}{10}$

$3\frac{7}{10}$

Correct answer:

$10\frac{1}{5}$

Explanation:

In the part of the midpoint formula

$x_{M}= \frac{x_{1} + x_{2} }{2}$ ,

set $x_{M}= 6\frac{1}{2}, x_{2}= 2\frac{4}{5}$ , and solve:

$x_{M}= \frac{x_{1} + x_{2} }{2}$

$6\frac{1}{2}= \frac{x_{1} + 2\frac{4}{5} }{2}$

$6\frac{1}{2} \cdot 2 = x_{1} + 2\frac{4}{5}$

$x_{1} + 2\frac{4}{5} = 13$

$x_{1} = 10\frac{1}{5}$

This is the correct -coordinate.

Report an Error

Example Question #1 : How To Find The Endpoints Of A Line Segment

One endpoint of a line segment on the coordinate plane is the point $\left (8.32, -4.29 \right )$ ; the midpoint of the segment is the point (-1.89, 8.56) . Give the -coordinate of the other endpoint of the segment.

Possible Answers:

3.215

-12.85

-12.1

21.41

2.135

Correct answer:

21.41

Explanation:

Using the part of the midpoint formula

$y_{M}= \frac{y_{1} + y_{2} }{2}$ .

set $y_{M}=8.56, y_{2}= -4.29$ and solve:

$8.56= \frac{y_{1} -4.29 }{2}$

$y_{1} -4.29 = 17.12$

$y_{1} = 21.41$

The second endpoint is ( -12.1, 21.41) .

Report an Error

Example Question #12 : Midpoint Formula

On the coordinate plane, is the midpoint of $\overline{AB}$ and is the midpoint of $\overline{AM}$ . has coordinates (288, 108) and has coordinates $\left ( 176, 300\right )$ .

Give the -coordinate of .

Possible Answers:

876

102

156

Correct answer:

876

Explanation:

First, find the -coordinate of . In the part of the midpoint formula

$y_{M}= \frac{y_{1} + y_{2} }{2}$ ,

set $y_{M}=300, y_{2}= 108$ , and solve:

$300= \frac{y_{1} + 108}{2}$

$y_{1} + 108 = 600$

$y_{1} =492$

Now, find the -coordinate of similarly, setting

$y_{M}= 492,y_{2}= 108$

$492= \frac{y_{1} + 108}{2}$

$y_{1} + 108= 984$

$y_{1} = 876$

This is the correct response.

Report an Error

Example Question #3 : How To Find The Endpoints Of A Line Segment

On the coordinate plane, is the midpoint of $\overline{AB}$ and is the midpoint of $\overline{AM}$ . has coordinates $\left (4\frac{1}{3},-12\frac{1}{2} \right )$ and has coordinates $\left ( -7 \frac{5}{6}, 6\frac{1}{3}\right )$ .

Give the -coordinate of .

Possible Answers:

$-44\frac{1}{3}$

$62\frac{5}{6}$

$40\frac{5}{6}$

$1\frac{1}{4}$

Correct answer:

$-44\frac{1}{3}$

Explanation:

First, find the -coordinate of . In the part of the midpoint formula

$x_{M}= \frac{x_{1} + x_{2} }{2}$ ,

set $x_{M}= -7 \frac{5}{6}, x_{2}= 4\frac{1}{3}$ , and solve:

$-7 \frac{5}{6}= \frac{x_{1} + 4\frac{1}{3}}{2}$

$x_{1} + 4\frac{1}{3}= -7 \frac{5}{6} \cdot 2$

$x_{1} + 4\frac{1}{3}= -15 \frac{2}{3}$

$x_{1} = -15 \frac{2}{3} - 4\frac{1}{3}$

$x_{1} = -20$

Now, find the -coordinate of similarly, setting

$x_{M}= -20, x_{2}= 4\frac{1}{3}$

$-20 = \frac{x_{1} + 4\frac{1}{3}}{2}$

$x_{1} + 4\frac{1}{3}= -20 \cdot 2$

$x_{1} + 4\frac{1}{3}= -40$

$x_{1} = -40 - 4\frac{1}{3}$

$x_{1} = -44\frac{1}{3}$

This is the correct response.

Report an Error

Example Question #13 : Midpoint Formula

Give the -coordinate of .

Possible Answers:

$-44\frac{1}{3}$

$-24\frac{2}{3}$

$37\frac{5}{6}$

$-50\frac{1}{6}$

$62\frac{5}{6}$

Correct answer:

$62\frac{5}{6}$

Explanation:

First, find the -coordinate of . In the part of the midpoint formula

$y_{M}= \frac{y_{1} + y_{2} }{2}$ ,

set $y_{M}=6\frac{1}{3}, y_{2}= -12\frac{1}{2}$ , and solve:

$6\frac{1}{3}= \frac{y_{1} -12\frac{1}{2} }{2}$

$y_{1} -12\frac{1}{2}= 6\frac{1}{3} \cdot 2$

$y_{1} -12\frac{1}{2}=12 \frac{2}{3}$

$y_{1} =12 \frac{2}{3} + 12\frac{1}{2}$

$y_{1} = 25\frac{1}{6}$

Now, find the -coordinate of similarly, setting

$y_{M}=25\frac{1}{6}, y_{2}= -12\frac{1}{2}$

$25\frac{1}{6}= \frac{y_{1} -12\frac{1}{2} }{2}$

$y_{1} -12\frac{1}{2} = 25\frac{1}{6} \cdot 2$

$y_{1} -12\frac{1}{2} = 50\frac{1}{3}$

$y_{1} = 50\frac{1}{3} +12\frac{1}{2}$

$y_{1} = 62\frac{5}{6}$

This is the correct response.

Report an Error

Example Question #181 : Geometry

On the coordinate plane, is the midpoint of $\overline{AB}$ and is the midpoint of $\overline{AM}$ . has coordinates (288, 108) and has coordinates $\left ( 176, 300\right )$ .

Give the -coordinate of .

Possible Answers:

736

116

204

684

Correct answer:

Explanation:

First, find the -coordinate of . In the part of the midpoint formula using the coordinates from and

$x_{M}= \frac{x_{1} + x_{2} }{2}$ ,

set $x_{M}= 176, x_{2}= 288$ , and solve:

$176= \frac{x_{1} + 288}{2}$

$x_{1} + 288 = 352$

$x_{1} =64$

Now, find the -coordinate of similarly, setting

$x_{M}= 64, x_{2}= 288$

$64= \frac{x_{1} + 288}{2}$

$x_{1} + 288 = 128$

$x_{1} = -160$

This is the correct response.

Report an Error

Example Question #181 : Geometry

Which of the following lines is parallel to y=9x-2 ?

Possible Answers:

y=-9x+2

$y=\frac{1}{9}x-8$

y=9x-8

$y=-\frac{1}{9}x-2$

Correct answer:

y=9x-8

Explanation:

Lines that are parallel must have the same slope. Thus, the correct answer must also have a slope of .

Report an Error

Example Question #2 : Parallel Lines

Which of the following lines is parallel to the line 2x-y=4 ?

Possible Answers:

$y=\frac{1}{2}x+3$

y=-2x-1

y=2x-1

$y=-\frac{1}{2}x-8$

Correct answer:

y=2x-1

Explanation:

First, put the equation in the more familiar y=mx+b format to see what the slope of the given line is.

2x-y=4

y=2x-4

Lines that are parallel must have the same slope. Thus, the correct answer must also have a slope of .

Report an Error

View SSAT- Upper Level Tutors

Joseph
Certified Tutor

CUNY College of Staten Island, Bachelor in Arts, Applied Psychology. New York University, Master of Arts, Applied Psychology.

View SSAT- Upper Level Tutors

Keith
Certified Tutor

Xavier University, Bachelor in Business Administration, Accounting. Ohio University-Main Campus, Masters in Education, Mathem...

View SSAT- Upper Level Tutors

Denisha
Certified Tutor

Nova Southeastern University, Doctor of Medicine, Ayurvedic Medicine. Nova Southeastern University, Master in Public Health, ...

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Statistics Tutors in San Francisco-Bay Area, Spanish Tutors in San Diego, Chemistry Tutors in Phoenix, ISEE Tutors in Miami, ISEE Tutors in San Francisco-Bay Area, GMAT Tutors in Philadelphia, Statistics Tutors in Seattle, GMAT Tutors in Los Angeles, Calculus Tutors in Los Angeles, Algebra Tutors in San Francisco-Bay Area

Popular Courses & Classes

Spanish Courses & Classes in Atlanta, MCAT Courses & Classes in Houston, GRE Courses & Classes in Boston, GRE Courses & Classes in New York City, ISEE Courses & Classes in Chicago, SAT Courses & Classes in Seattle, SSAT Courses & Classes in Chicago, GMAT Courses & Classes in Chicago, ISEE Courses & Classes in San Diego, SSAT Courses & Classes in Houston

Popular Test Prep

SAT Test Prep in Denver, SSAT Test Prep in Phoenix, ACT Test Prep in Atlanta, GMAT Test Prep in Seattle, MCAT Test Prep in Washington DC, ISEE Test Prep in Houston, MCAT Test Prep in Boston, SSAT Test Prep in Washington DC, SAT Test Prep in Miami, GMAT Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : SSAT Upper Level Quantitative (Math)

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #1 : How To Find The Endpoints Of A Line Segment

Example Question #171 : Geometry

Example Question #121 : Coordinate Geometry

Example Question #1 : How To Find The Endpoints Of A Line Segment

Example Question #12 : Midpoint Formula

Example Question #3 : How To Find The Endpoints Of A Line Segment

Example Question #13 : Midpoint Formula

Example Question #181 : Geometry

Example Question #181 : Geometry

Example Question #2 : Parallel Lines

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: