Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : Triangles

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #135 : Sat Mathematics

Solve each problem and decide which is the best of the choices given.

Solve for .

Untitled

Possible Answers:

x=20

x=180

x=60

x=120

x=40

Correct answer:

x=20

Explanation:

To solve for , you must first solve for .

All triangles' angles add up to $180$^{\circ}$$ .

So subtract (40+20) from 180 to get 120 , the value of .

Angles and are supplementary, meaning they add up to 180 .

Subtract 180 from 120 to get $60$^{\circ}$$ .

$3x=60$^{\circ}$$ , so $x=20$^{\circ}$$ .

Report an Error

Example Question #136 : Sat Mathematics

Triangle 2

Refer to the above figure. Evaluate $m \angle CDE$ .

Possible Answers:

$144^{\circ }$

$150 ^{\circ }$

$120^{\circ}$

$162 ^{\circ }$

$135^{\circ }$

Correct answer:

$150 ^{\circ }$

Explanation:

$\bigtriangleup ABC$ is marked with three congruent sides, making it an equilateral triangle, so $m \angle ABC = 60 ^{\circ }$ . This is an exterior angle of $\bigtriangleup BCD$ , making its measure the sum of those of its remote interior angles; that is,

$m \angle BCD + m \angle BDC = m \angle ABC$

$\bigtriangleup BCD$ has congruent sides $\overline{BC}$ and $\overline{CD}$ , so, by the Isosceles Triangle Theorem, $m \angle BCD = m \angle BDC$ . Substituting $m \angle BDC$ for $m \angle BCD$ and $60 ^{\circ }$ for $m \angle ABC$ :

$m \angle BDC + m \angle BDC = 60 ^{\circ }$

$2 \cdot m \angle BDC = 60 ^{\circ }$

$m \angle BDC = 30 ^{\circ }$

$\angle BDC$ and $\angle CDE$ form a linear pair and are therefore supplementary - that is, their degree measures total $180 ^{\circ }$ . Setting up the equation

$m \angle BDC + m\angle CDE= 180 ^{\circ }$

and substituting:

$30 ^{\circ } + m\angle CDE= 180 ^{\circ }$

$m\angle CDE= 150 ^{\circ }$

Report an Error

Example Question #132 : Plane Geometry

Equilateral

Figure is not drawn to scale.

Refer to the provided figure. Evaluate $m \angle CAD$ .

Possible Answers:

$13^{\circ}$

$18^{\circ }$

$8^{\circ }$

$28^{\circ }$

$23^{\circ }$

Correct answer:

$18^{\circ }$

Explanation:

$\bigtriangleup ABC$ is an equilateral, so all of its angles - in particular, $\angle ACB$ - measure $60^{\circ }$ . This angle is an exterior angle to $\bigtriangleup DAC$ , and its measure is equal to the sum of those of its two remote interior angles, $\angle DAC$ and $\angle D$ , so

$m\angle DAC + m\angle D = m \angle ACB$

Setting $m \angle ACB =60^{ \circ}$ and $m \angle D = 42^{\circ }$ , solve for $m\angle DAC$ :

$m\angle DAC + 42^{\circ }= 60^{\circ }$

$m\angle DAC = 60^{\circ } - 42^{\circ }= 18^{\circ }$

Report an Error

Example Question #1 : Acute / Obtuse Triangles

If a = 7 and b = 4, which of the following could be the perimeter of the triangle?

Msp30320bea9chb26d18hh0000627i1e4ibba8c4f5

I. 11

II. 15

III. 25

Possible Answers:

I Only

I and II Only

II Only

II and III Only

I, II and III

Correct answer:

II Only

Explanation:

Consider the perimeter of a triangle:

P = a + b + c

Since we know a and b, we can find c.

In I:

11 = 7 + 4 + c

11 = 11 + c

c = 0

Note that if c = 0, the shape is no longer a trial. Thus, we can eliminate I.

In II:

15 = 7 + 4 + c

15 = 11 + c

c = 4.

This is plausible given that the other sides are 7 and 4.

In III:

25 = 7 + 4 + c

25 = 11 + c

c = 14.

It is not possible for one side of a triangle to be greater than the sum of both of the other sides, so eliminate III.

Thus we are left with only II.

Report an Error

Example Question #141 : Sat Mathematics

Which of the following measurements can NOT represent the sides of a triangle.

Possible Answers:

12, 13, 26

2, 3, 4

7, 8, 17

10, 14, 25

3, 5, 6

Correct answer:

12, 13, 26

Explanation:

Given the Triangle Inequality, the sum of any two sides of a triangle must be greater than the third side.

Given the measurements 12, 13, 26 :

$12 + 13 \ngtr 26$

Therefore, these lengths cannot represent a triangle.

Report an Error

Example Question #142 : Sat Mathematics

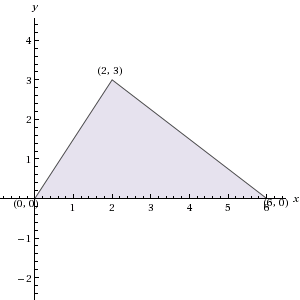
If triangle ABC has vertices (0, 0), (6, 0), and (2, 3) in the xy-plane, what is the area of ABC?

Possible Answers:

Correct answer:

Explanation:

Sketching ABC in the xy-plane, as pictured here, we see that it has base 6 and height 3. Since the formula for the area of a triangle is 1/2 * base * height, the area of ABC is 1/2 * 6 * 3 = 9.

Report an Error

Example Question #141 : Geometry

The height, , of triangle PQR in the figure is one-fourth the length of . In terms of h, what is the area of triangle PQR ?

Possible Answers:

$h^{2}$

$2h^{2}$

$\frac{1}{2}h^{2}$

$3h^{2}$

Correct answer:

$2h^{2}$

Explanation:

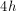
If $\dpi{100} \small h=\frac{1}{4}$ * $\dpi{100} \small \overline{PQ}$ , then the length of $\dpi{100} \small \overline{PQ}$ must be $\dpi{100} \small 4h$ .

Using the formula for the area of a triangle ( $\frac{1}{2}bh$ ), with $\dpi{100} \small b=4h$ , the area of the triangle must be $2h^{2}$ .

Report an Error

Example Question #1 : How To Find The Height Of An Acute / Obtuse Triangle

Find the height of a triangle if the area of the triangle = 18 and the base = 4.

Possible Answers:

Correct answer:

Explanation:

The area of a triangle = (1/2)bh where b is base and h is height. 18 = (1/2)4h which gives us 36 = 4h so h =9.

Report an Error

Example Question #141 : Sat Mathematics

$\text{Triangle A}$ and $\text{Triangle B}$ are similar triangles. The perimeter of Triangle A is 45” and the length of two of its sides are 15” and 10”. If the perimeter of Triangle B is 135” and what are lengths of two of its sides?

Possible Answers:

${13}''\textup{ and }{19}''$

${4}''\textup{ and }{6}''$

${30}''\textup{ and }{45}''$

${20}''\textup{ and }{30}''$

Correct answer:

${30}''\textup{ and }{45}''$

Explanation:

The perimeter is equal to the sum of the three sides. In similar triangles, each side is in proportion to its correlating side. The perimeters are also in equal proportion.

Perimeter A = 45” and perimeter B = 135”

The proportion of Perimeter A to Perimeter B is 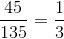$\frac{45}{135}=\frac{1}{3}$ .

This applies to the sides of the triangle. Therefore to get the any side of Triangle B, just multiply the correlating side by 3.

15” x 3 = 45”

10” x 3 = 30“

Screen shot 2016 02 16 at 10.45.30 am

Report an Error

Example Question #1 : How To Find The Length Of The Side Of An Acute / Obtuse Triangle

A triangle has sides of length 8, 13, and L. Which of the following cannot equal L?

Possible Answers:

Correct answer:

Explanation:

The sum of the lengths of two sides of a triangle cannot be less than the length of the third side. 8 + 4 = 12, which is less than 13.

Report an Error

View SAT Mathematics Tutors

Clinton
Certified Tutor

Rensselaer Polytechnic Institute, Current Undergrad, Biology, General. Albany Medical College, PHD, Molecular and Cellular Ph...

View SAT Mathematics Tutors

Troy
Certified Tutor

Rice University, Bachelor in Arts, Kinesiology.

View SAT Mathematics Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

ACT Courses & Classes in Phoenix, ACT Courses & Classes in Denver, Spanish Courses & Classes in Chicago, MCAT Courses & Classes in Philadelphia, ACT Courses & Classes in Atlanta, Spanish Courses & Classes in Seattle, LSAT Courses & Classes in New York City, SSAT Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in San Diego, SAT Courses & Classes in Washington DC

Popular Test Prep

SAT Test Prep in Chicago, ACT Test Prep in Denver, SAT Test Prep in Boston, SAT Test Prep in New York City, GMAT Test Prep in San Francisco-Bay Area, GRE Test Prep in New York City, GMAT Test Prep in Boston, LSAT Test Prep in San Diego, ACT Test Prep in Phoenix, ACT Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : Triangles

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #135 : Sat Mathematics

Example Question #136 : Sat Mathematics

Example Question #132 : Plane Geometry

Example Question #1 : Acute / Obtuse Triangles

Example Question #141 : Sat Mathematics

Example Question #142 : Sat Mathematics

Example Question #141 : Geometry

Example Question #1 : How To Find The Height Of An Acute / Obtuse Triangle

Example Question #141 : Sat Mathematics

Example Question #1 : How To Find The Length Of The Side Of An Acute / Obtuse Triangle

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: