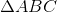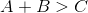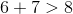An equilateral triangle has three congruent sides and results in three congruent angles. This figure results in two special right triangles back to back: 30° – 60° – 90° giving sides of x - x √3 – 2x in general. The height of the triangle is the x √3 side.  So A_triangle = 1/2 bh = 1/2 * 12 * 6√3 = 36√3 cm².

Recall that an equilateral triangle also obeys the rules of isosceles triangles.   That means that our triangle can be represented as having a height that bisects both the opposite side and the angle from which the height is "dropped."  For our triangle, this can be represented as:

Now, although we do not yet know the height, we do know from our 30-60-90 regular triangle that the side opposite the 60° angle is √3 times the length of the side across from the 30° angle. Therefore, we know that the height is 3√3.

Now, the area of a triangle is (1/2)bh. If the height is 3√3 and the base is 6, then the area is (1/2) * 6 * 3√3 = 3 * 3√3 = 9√(3).

Perimeter of hexagon =  = perimeter of triangle

 = side of the triangle

The sum of the lengths of any two sides of a triangle must be greater than the length of third side.

Therefore, because 

and

, the correct answer must be .

The sum of the angles in a triangle is 180^o:  a + b + c = 180

In this case, the average of a and b is 75:

(a + b)/2 = 75, then multiply both sides by 2

(a + b) = 150, then substitute into first equation

150 + c = 180

c = 30

In a triangle, there can only be one obtuse angle. Additionally, all the angle measures must add up to 180.

The measures of the three angles are x, y, and z. Because the sum of the measures of the angles in any triangle must be 180 degrees, we know that x + y + z = 180. We can use this equation, along with the other two equations given, to form this system of equations:

x + y + z = 180

y = 2z

z = 0.5x - 30

If we can solve for both y and x in terms of z, then we can substitute these values into the first equation and create an equation with only one variable.

Because we are told already that y = 2z, we alreay have the value of y in terms of z.

We must solve the equation z = 0.5x - 30 for x in terms of z.

Add thirty to both sides.

z + 30 = 0.5x

Mutliply both sides by 2

2(z + 30) = 2z + 60 = x

x = 2z + 60

Now we have the values of x and y in terms of z. Let's substitute these values for x and y into the equation x + y + z = 180.

(2z + 60) + 2z + z = 180

5z + 60 = 180

5z = 120

z = 24

Because y = 2z, we know that y = 2(24) = 48. We also determined earlier that x = 2z + 60, so x = 2(24) + 60 = 108.

Thus, the measures of the three angles of the triangle are 24, 48, and 108. The question asks for the largest of these measures, which is 108.

The answer is 108. 

The answer is 18

We know that the sum of all the angles is 180. Using the rest of the information given we can write the other two equations:

x + y + z = 180      

x = 3y      

2x = z

We can solve for y and z in the second and third equations and then plug into the first to solve.

x + (1/3)x + 2x = 180

3[x + (1/3)x + 2x = 180]

3x + x + 6x = 540

10x = 540

x = 54

y = 18

z = 108

A straight line segment has 180 degrees. Therefore, the angle that is not labelled must have:

We know that the sum of the angles in a triangle is 180 degrees. As a result, we can set up the following algebraic equation:

Subtract 70 from both sides:

Divide by 2:

Since the sum of the angles of a triangle is , we know that 

.

So 

and .