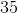All SAT Math Resources
Example Questions
Example Question #91 : Right Triangles
A traffic light hangs t feet from the ground, over a street. A man standing the shadow of the traffic light is h feet tall, and his shadow is s feet long. How far is the man standing from the spot on the street directly under the traffic light?
We can set this problem up like a set of similar triangles.
The first triangle is created by the three points: The Traffic light, the spot beneath the traffic light, and the spot where the man is standing (which is also the spot where the traffic light's shadow is).
The height of this Triangle is "T" as given in the question, and its base is the part that we are asked to solve for.
The second triangle is created by the top of the man's head, his feet, and the end of his shadow.
The height of this Triangle is "h" as given in the questions, and the base is "s".
We set up a proportion:
where X is the distance we are asked to find. Simply cross-multiply to solve.
Example Question #91 : Right Triangles

An meteor crashed in the desert and created an oblong shaped crater. Scientists want to find the width 

To calculate the width of the crater, use the given information to establish that the image draws similar triangles. When triangles that have corresponding angles and a ratio to their side lengths they are considered to be similar triangles.
Identify the known information.
therefore,

and the bases of the triangles are parallel.
Also,
Set up the side ratios for this particular problem.
Looking at the only full ratio that is given, the scalar multiplier can be found.
Therefore, to find the width of the crater 

Example Question #93 : Right Triangles
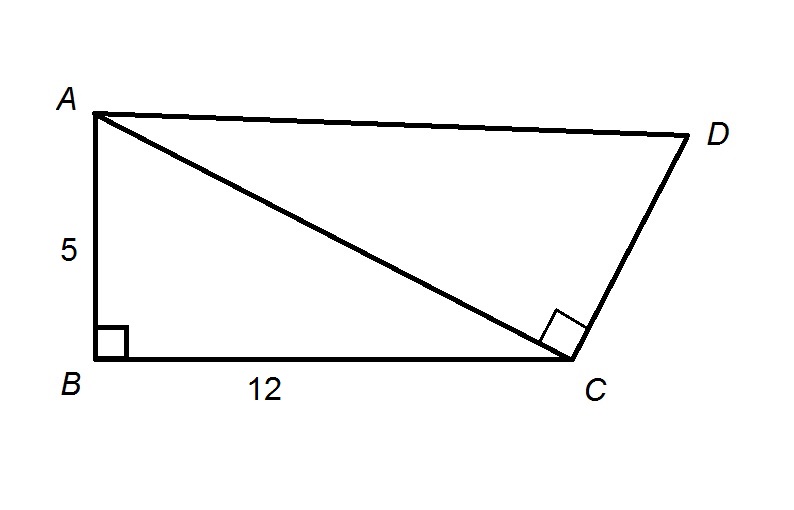
In the given diagram, 
By the Pythagorean Theorem,
Set 

Take the positive square root of both sides:

Set 

A right triangle has as its area half the product of the length of its legs, so the area of 
To the nearest whole number, this rounds to 35.
Example Question #211 : Triangles
A square rug border consists of a continuous pattern of equilateral triangles, with isosceles triangles as corners, one of which is shown above. If the length of each equilateral triangle side is 5 inches, and there are 40 triangles in total, what is the total perimeter of the rug?
The inner angles of the corner triangles is 30°.
180
124
200
188
208
188
There are 2 components to this problem. The first, and easier one, is recognizing how much of the perimeter the equilateral triangles take up—since there are 40 triangles in total, there must be 40 – 4 = 36 of these triangles. By observation, each contributes only 1 side to the overall perimeter, thus we can simply multiply 36(5) = 180" contribution.
The second component is the corner triangles—recognizing that the congruent sides are adjacent to the 5-inch equilateral triangles, and the congruent angles can be found by
180 = 30+2x → x = 75°
We can use ratios to find the unknown side:
75/5 = 30/y → 75y = 150 → y = 2''.
Since there are 4 corners to the square rug, 2(4) = 8'' contribution to the total perimeter. Adding the 2 components, we get 180+8 = 188 inch perimeter.
Example Question #215 : Triangles
The height of an equilateral triangle is
What is the triangle's perimeter?
24
6
12
8
12
An altitude drawn in an equilateral triangle will form two 30-60-90 triangles. The height of equilateral triangle is the length of the longer leg of the 30-60-90 triangle. The length of the equilateral triangle's side is the length of the hypotenuse of the 30-60-90.
The ratio of the length of the hypotenuse to the length of the longer leg of a 30-60-90 triangle is 
The length of the longer leg of the 30-60-90 triangle in this problem is
Using this ratio, we find that the length of this triangle's hypotenuse is 4. Thus the perimeter of the equilateral triangle will be 4 multiplied by 3, which is 12.
Example Question #121 : Geometry
A triangle has a base of 5 cm and an area of 15 cm. What is the height of the triangle?
5 cm
3 cm
None of the above
6 cm
1.5 cm
6 cm
The area of a triangle is (1/2)*base*height. We know that the area = 15 cm, and the base is 5 cm, so:
15 = 1/2 * 5 * height
3 = 1/2 * height
6 = height
Example Question #542 : Geometry
In the figure above, AB = AD = AE = BD = BC = CD = DE = 1. What is the distance from A to C?
Example Question #121 : Geometry
A triangles has sides of 5, 9, and 

The sum of the lengths of the shortest sides of a triangle cannot be less than the third side.
3 + 5 = 8 < 9, so 3 can't be a value of x.
Example Question #4 : How To Find The Height Of A Triangle
An equilateral triangle has a side length of 4. What is the height of the triangle?
Because the triangle is an equilateral triangle, you know that all sides have the same length, so all sides have the length of 4. Draw the triangle and label all sides as 4. Next, draw a point in the middle of one of the sides, and label each side as 2. Draw a line segment from the midpoint that you just created to the opposite angle of the triangle. That line segment is the height of the triangle. You can solve for it by using the Pythagorean theorem.
The Pythagorean theorem states that
In our scenario a = 2, c = 4, and you are solving for b. After plugging the numbers into the formula you get

and then
and then
and then
Therefore, the height of the triangle is 
Example Question #1 : Equilateral Triangles
The area of square ABCD is 50% greater than the perimeter of the equilateral triangle EFG. If the area of square ABCD is equal to 45, then what is the area of EFG?
25
50
50√3
25√3
30
25√3
If the area of ABCD is equal to 45, then the perimeter of EFG is equal to x * 1.5 = 45. 45 / 1.5 = 30, so the perimeter of EFG is equal to 30. This means that each side is equal to 10.
The height of the equilateral triangle EFG creates two 30-60-90 triangles, each with a hypotenuse of 10 and a short side equal to 5. We know that the long side of 30-60-90 triangle (here the height of EFG) is equal to √3 times the short side, or 5√3.
We then apply the formula for the area of a triangle, which is 1/2 * b * h. We get 1/2 * 10 * 5√3 = 5 * 5√3 = 25√3.
In general, the height of an equilateral triangle is equal to √3 / 2 times a side of the equilateral triangle. The area of an equilateral triangle is equal to 1/2 * √3s/ 2 * s = √3s2/4.
All SAT Math Resources