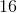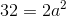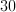We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : Triangles

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #152 : Geometry

Which of the given answers choices could NOT represent the sides of a triangle?

Possible Answers:

4, 5, 10

2, 2, 3

5, 6, 10

10, 10, 19

All of the given answers could represent the sides of a triangle.

Correct answer:

4, 5, 10

Explanation:

In order for three lengths to represent the sides of a triangle, they must pass the Triangle Inequality.

a + b >c

This means that the sum of any two sides of the triangle must exceed the length of the third side.

With the given answers, the one set of lengths that fail this test is 4, 5, 10 .

$4+5 \ngtr 10$

Therefore, the lengths 4, 5, 10 could not represent the sides of a triangle.

Report an Error

Example Question #1 : 45/45/90 Right Isosceles Triangles

An isosceles triangle has a base of 6 and a height of 4. What is the perimeter of the triangle?

Possible Answers:

None of these

Correct answer:

Explanation:

An isosceles triangle is basically two right triangles stuck together. The isosceles triangle has a base of 6, which means that from the midpoint of the base to one of the angles, the length is 3. Now, you have a right triangle with a base of 3 and a height of 4. The hypotenuse of this right triangle, which is one of the two congruent sides of the isosceles triangle, is 5 units long (according to the Pythagorean Theorem).

The total perimeter will be the length of the base (6) plus the length of the hypotenuse of each right triangle (5).

5 + 5 + 6 = 16

Report an Error

Example Question #5 : 45/45/90 Right Isosceles Triangles

What is the area of a square that has a diagonal whose endpoints in the coordinate plane are located at (-8, 6) and (2, -4)?

Possible Answers:

100

100√2

200√2

50√2

Correct answer:

100

Explanation:

Square_part1

Square_part2

Square_part3

Report an Error

Example Question #1 : Isosceles Triangles

The length of the diagonal of a given square is $4\sqrt{2}$ . What is the square's area?

Possible Answers:

Correct answer:

Explanation:

If we divide the square into two triangles via its diagonal, then we know that the length of the diagonal is equal to the length of the triangles' hypotenuse.

We can use the Pythagorean Theorem to find the length of the two sides of one of our triangles.

c^2 = a^2 + b^2

Since we're dealing with a square, we know that the two sides of the square (which are the same as the two sides of one of our triangles) will be equal to one another. Therefore, we can say:

$(4\sqrt{2})^2 = 2a^2$

Now, solve for the unknown:

32 = 2a^2

16 = a^2

4=a .

This means that the length of the sides of our triangle, as well as the sides of our square, is .

To find the area of the square, do the following:

$A = l\cdot w = 4 \cdot 4 = 16$ .

Report an Error

Example Question #131 : Triangles

Two sides of an isosceles triangle are 20 and 30. What is the difference of the largest and the smallest possible perimeters?

Possible Answers:

The answer cannot be determined

Correct answer:

Explanation:

The trick here is that we don't know which is the repeated side. Our possible triangles are therefore 20 + 20 + 30 = 70 or 30 + 30 + 20 = 80. The difference is therefore 80 – 70 or 10.

Report an Error

Example Question #11 : Acute / Obtuse Isosceles Triangles

A triangle with two equal angles is called a(n) __________.

Possible Answers:

disjoint triangle

equilateral triangle

Pythagoras triangle

right triangle

isosceles triangle

Correct answer:

isosceles triangle

Explanation:

An isoceles triangle is a triangle that has at least two congruent sides (and therefore, at least two congruent angles as well).

Report an Error

Example Question #4 : Isosceles Triangles

Triangle ABC has angle measures as follows:

$\dpi{100} \small m\angle ABC=4x+3$

$\dpi{100} \small m\angle ACB=2x+6$

$\dpi{100} \small m\angle BAC=3x$

What is $\dpi{100} \small m\angle BAC$ ?

Possible Answers:

Correct answer:

Explanation:

The sum of the measures of the angles of a triangle is 180.

Thus we set up the equation $\dpi{100} \small 4x+3+2x+6+3x=180$

After combining like terms and cancelling, we have $\dpi{100} \small 9x=171\rightarrow x=19$

Thus $\dpi{100} \small m\angle BAC=3x=57$

Report an Error

Example Question #5 : Isosceles Triangles

The base angle of an isosceles triangle is five more than twice the vertex angle. What is the base angle?

Possible Answers:

$62$

$34$

$47$

$55$

$73$

Correct answer:

$73$

Explanation:

Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.

Let $x$ = the vertex angle and $2x+5$ = the base angle

So the equation to solve becomes $x+(2x+5)+(2x+5)=180$

Thus the vertex angle is 34 and the base angles are 73.

Report an Error

Example Question #6 : Isosceles Triangles

The base angle of an isosceles triangle is 15 less than three times the vertex angle. What is the vertex angle?

Possible Answers:

Correct answer:

Explanation:

Every triangle contains 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.

Let = vertex angle and 3x-15 = base angle

So the equation to solve becomes x+(3x-15)+(3x-15)=180 .

Report an Error

Example Question #4 : Isosceles Triangles

The base angle of an isosceles triangle is ten less than twice the vertex angle. What is the vertex angle?

Possible Answers:

$70^{\circ}$

$35^{\circ}$

$20^{\circ}$

$40^{\circ}$

$65^{\circ}$

Correct answer:

$40^{\circ}$

Explanation:

Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.

Let = vertex angle and 2x - 10 = base angle

So the equation to solve becomes x + (2x - 10) + (2x - 10) = 180

So the vertex angle is 40 and the base angles is 70

Report an Error

View SAT Mathematics Tutors

Momeena
Certified Tutor

State University of New York at New Paltz, Bachelors, Mathematics & Elementary Education. State University of New York at New...

View SAT Mathematics Tutors

Stephen
Certified Tutor

Grinnell College, Bachelor in Arts, Computer Science.

View SAT Mathematics Tutors

Scott
Certified Tutor

Rutgers College, Bachelors, Political Science and Government. Florida Coastal School of Law, PHD, Law.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

ISEE Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Philadelphia, SSAT Courses & Classes in Chicago, LSAT Courses & Classes in Phoenix, MCAT Courses & Classes in Boston, MCAT Courses & Classes in San Diego, MCAT Courses & Classes in Phoenix, ACT Courses & Classes in Boston

Popular Test Prep

SAT Test Prep in Los Angeles, GMAT Test Prep in Philadelphia, MCAT Test Prep in Phoenix, ISEE Test Prep in Phoenix, ISEE Test Prep in Philadelphia, SSAT Test Prep in Phoenix, GMAT Test Prep in Phoenix, ACT Test Prep in Denver, LSAT Test Prep in Philadelphia, SAT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : Triangles

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #152 : Geometry

Example Question #1 : 45/45/90 Right Isosceles Triangles

Example Question #5 : 45/45/90 Right Isosceles Triangles

Example Question #1 : Isosceles Triangles

Example Question #131 : Triangles

Example Question #11 : Acute / Obtuse Isosceles Triangles

Example Question #4 : Isosceles Triangles

Example Question #5 : Isosceles Triangles

Example Question #6 : Isosceles Triangles

Example Question #4 : Isosceles Triangles

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: