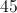SAT Math : Triangles
Study concepts, example questions & explanations for SAT Math
All SAT Math Resources
Example Questions
Example Question #8 : Isosceles Triangles
The base angle of an isosceles triangle is 10 more than twice the vertex angle. What is the vertex angle?
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 
So the equation to solve becomes
The vertex angle is 32 degrees and the base angle is 74 degrees
Example Question #1 : Isosceles Triangles
In an isosceles triangle, the vertex angle is 15 less than the base angle. What is the base angle?
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 
So the equation to solve becomes
Thus, 65 is the base angle and 50 is the vertex angle.
Example Question #2 : Isosceles Triangles
In an isosceles triangle the vertex angle is half the base angle. What is the vertex angle?
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 
So the equation to solve becomes 
Example Question #3 : Isosceles Triangles
If the average (arithmetic mean) of two noncongruent angles of an isosceles triangle is 
Since the triangle is isosceles, we know that 2 of the angles (that sum up to 180) must be equal. The question states that the noncongruent angles average 55°, thus providing us with a system of two equations:
Solving for x and y by substitution, we get x = 70° and y = 40° (which average out to 55°).
70 + 70 + 40 equals 180 also checks out.
Since 70° is not an answer choice for us, we know that the 40° must be one of the angles.
Example Question #4 : Isosceles Triangles
The base angle of an isosceles triangle is 
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Solve the equation 
x = 180 - 27 - 27
x = 126
Therefore the measure of the vertex angle is 
Example Question #11 : Isosceles Triangles
An isosceles triangle has an area of 12. If the ratio of the base to the height is 3:2, what is the length of the two equal sides?
3√3
6
4
5
4√3
5
Area of a triangle is ½ x base x height. Since base:height = 3:2, base = 1.5 height. Area = 12 = ½ x 1.5 height x height or 24/1.5 = height2. Height = 4. Base = 1.5 height = 6. Half the base and the height form the legs of a right triangle, with an equal leg of the isosceles triangle as the hypotenuse. This is a 3-4-5 right triangle.
Example Question #12 : Isosceles Triangles
Two sides of a triangle each have length 6. All of the following could be the length of the third side EXCEPT
This question is about the Triangle Inequality, which states that in a triangle with two sides A and B, the third side must be greater than the absolute value of the difference between A and B and smaller than the sum of A and B.
Applying the Triangle Inequality to this problem, we see that the third side must be greater than the absolute value of the difference between the other two sides, which is |6-6|=0, and smaller than the sum of the two other sides, which is 6+6=12. The only answer choice that does not satisfy this range of possible values is 12 since the third side must be LESS than 12.
Example Question #13 : Isosceles Triangles
A triangle has the following side lengths:
Which of the following correctly describes the triangle?
Obtuse and isosceles
Acute and isosceles
None of these
Obtuse and scalene
Acute and scalene
Acute and isosceles
The triangle has two sides of equal length, 13, so it is by definition isosceles.
To determine whether the triangle is acute, right, or obtuse, compare the sum of the squares of the lengths of the two shortest sides to the square of the length of the longest side. The former quantity is equal to
The latter quantity is equal to
The former is greater than the latter; consequently, the triangle is acute. The correct response is that the triangle is acute and isosceles.
All SAT Math Resources
