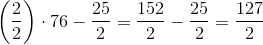Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : Fractions

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 3 4 5 6 7 8 9 … 18 19 Next →

Example Question #11 : Fractions

Order the following fractions from least to greatest:

$\frac{1}{6}, \frac{5}{7}, \frac{1}{3}, \frac{5}{6}$

Possible Answers:

$\frac{1}{3}, \frac{1}{6}, \frac{5}{6}, \frac{5}{7}$

$\frac{5}{6}, \frac{5}{7}, \frac{1}{3}, \frac{1}{6}$

$\frac{1}{6}, \frac{1}{3}, \frac{5}{7}, \frac{5}{6}$

$\frac{1}{6}, \frac{5}{7}, \frac{1}{3}, \frac{5}{6}$

$\frac{5}{7}, \frac{1}{6}, \frac{1}{3}, \frac{5}{6}$

Correct answer:

$\frac{1}{6}, \frac{1}{3}, \frac{5}{7}, \frac{5}{6}$

Explanation:

To solve this problem, let's find the least common denominator for our fractions.

$7\cdot6 = 42$

is the lowest number that each of our current denominators are factors of.

Now, let's rewrite each fraction so that its denominator is .

$\frac{1 \cdot 7}{6 \cdot7}, \frac{5\cdot6}{7\cdot6}, \frac{1\cdot14}{3 \cdot 14}, \frac{5\cdot7}{6\cdot7} = \frac{7}{42}, \frac{30}{42}, \frac{14}{42}, \frac{35}{42}$

Then we can rearrange these new fractions from least to greatest, keeping in mind what they're reduced forms were.

$\frac{7}{42}, \frac{14}{42}, \frac{30}{42}, \frac{35}{42}$

Then, by either simplifying these fractions or by remembering their original forms, we can see that the order of our fractions from least to greatest is:

$\frac{1}{6}, \frac{1}{3}, \frac{5}{7}, \frac{5}{6}$

Report an Error

Example Question #11 : How To Order Fractions From Least To Greatest Or From Greatest To Least

Which of the following fractions is the smallest?

1/3, 115/276, 112/350, 1050/3330, 0.75/2

Possible Answers:

$\frac{0.75}{2}$

$\frac{115}{276}$

$\frac{1050}{3330}$

$\frac{112}{350}$

$\frac{1}{3}$

Correct answer:

$\frac{1050}{3330}$

Explanation:

1/3, 115/276, 112/350, 1050/3330, 0.75/2

First you need to put the fractions in ascending order:

1050/3330, 112/350, 1/3, 0.75/2, 115/276

Then choose the fraction with the smallest value (1050/3330).

Report an Error

Example Question #13 : Fractions

Order from greatest to least:

$- \frac{3}{13}, - \frac{4}{17}, - \frac{5}{19}$

Possible Answers:

$- \frac{3}{13}> - \frac{4}{17}>- \frac{5}{19}$

$- \frac{4}{17}>- \frac{5}{19}>- \frac{3}{13}$

$- \frac{5}{19}> - \frac{4}{17}>- \frac{3}{13}$

$- \frac{3}{13}>- \frac{5}{19}> - \frac{4}{17}$

$- \frac{5}{19}>- \frac{3}{13}> - \frac{4}{17}$

Correct answer:

$- \frac{3}{13}> - \frac{4}{17}>- \frac{5}{19}$

Explanation:

Rewrite the numbers $- \frac{3}{13}, - \frac{4}{17}, - \frac{5}{19}$ in terms of the least common denominator, which is $13 \times 17 \times 19 = 4,199$ :

$- \frac{3}{13} = - \frac{3 \times 17 \times 19 }{13 \times 17 \times 19 } = - \frac{969}{4,199} = \frac{-969}{4,199}$

$- \frac{4}{17} = - \frac{4 \times 13 \times 19}{17 \times 13 \times 19 } = -\frac{988}{4,199} = \frac{-988}{4,199}$

$- \frac{5}{19} = - \frac{5 \times 13 \times 17 }{19 \times 13 \times 17} = -\frac{1,105}{4,199}= \frac{-1,105}{4,199}$

Comparing numerators, we see that

-969 > -988 > -1,105

It follows that

$\frac{-969}{4,199} >\frac{ -988}{4,199} >\frac{ -1,105}{4,199}$

and

$- \frac{3}{13}> - \frac{4}{17}>- \frac{5}{19}$ ,

making this the correct order.

Report an Error

Example Question #14 : Fractions

Order from least to greatest:

$\frac{4}{7} , \frac{5}{8}, \frac{7}{12}$

Possible Answers:

$\frac{4 }{7} <\frac{5}{8} < \frac{7}{12}$

$\frac{5}{8} < \frac{7}{12} < \frac{4 }{7}$

$\frac{5}{8} < \frac{4 }{7} < \frac{7}{12}$

$\frac{4 }{7} < \frac{7}{12} <\frac{5}{8}$

$\frac{7}{12} < \frac{5}{8} < \frac{4 }{7}$

Correct answer:

$\frac{4 }{7} < \frac{7}{12} <\frac{5}{8}$

Explanation:

Express all three fractions in terms of their least common denominator - the least common multiple of denominators 7, 8, and 12, which is 168. Do this by multiplying the numerator and denominator in each fraction by whatever number yields a product of 168 in the denominator.

$\frac{4 }{7} = \frac{4 \cdot 24 }{7 \cdot 24 } = \frac{96}{168}$

$\frac{5}{8} = \frac{5 \cdot 21 }{8 \cdot 21 } = \frac{105}{168 }$

$\frac{7}{12} = \frac{7 \cdot 14 }{12 \cdot 14 } = \frac{98}{168}$

96 < 98 < 105 ;

it follows that

$\frac{96}{168}< \frac{98}{168} < \frac{105}{168 }$ ,

$\frac{4 }{7} < \frac{7}{12} <\frac{5}{8}$

Report an Error

Example Question #11 : Fractions

Which of the following five numbers is the greatest?

Possible Answers:

$\frac{13}{17}$

$\frac{3}{4}$

$\frac{8}{11}$

$\frac{10}{13}$

$\frac{5}{7}$

Correct answer:

$\frac{10}{13}$

Explanation:

For each fraction, divide the numerator by the denominator. This is shown below for each fraction to three decimal places:

Division

From the decimal representations, $\frac{10}{13}$ can be seen to be the greatest of the five choices.

Report an Error

Example Question #16 : Fractions

Solve each problem and decide which is the best of the choices given.

There is a bag with green marbles, red marbles, purple marbles, and blue marbles. What is the probability that a red marble is randomly chosen from the bag?

Possible Answers:

$86.67\%$

$20\%$

$66.67\%$

$13.33 \%$

$6.67\%$

Correct answer:

$13.33 \%$

Explanation:

To find the probability of a red marble being randomly chosen, you have to divide the number of red marbles by the total number of marbles.

There are red, and 3+2+7+3=15 total,

thus, creating the fraction

$\frac{2}{15}{}$ .

To find the percentage, simply divide by and multiply the result by 100 to get $13.33\%$ .

Report an Error

Example Question #17 : Fractions

Determine the approximate percentage given the fraction $\frac{3}{7}$ .

Possible Answers:

$37\%$

$39\%$

$47\%$

$41\%$

$43\%$

Correct answer:

$43\%$

Explanation:

Because a fraction is a part of a whole $100\%$ , set up a proportion.

$\frac{3}{7}=\frac{x}{100}$

$x=\frac{300}{7}=42.857$

The fraction $\frac{3}{7}$ is approximately $43\%$ .

Report an Error

Example Question #18 : Fractions

Bob and Jill go eat dinner at a fancy restaurant. Bob gets lobster and Jill gets crab legs. The lobster cost $\$60.00$ , and the crab legs cost $\$ 50.00$ . If they leave $15\%$ tip, how much is the combined bill?

Possible Answers:

$\$126$

$\$126.50$

$\$110$

$\$110.50$

Correct answer:

$\$126.50$

Explanation:

To do this, we need to sum up each meal, and then convert the tip into a decimal.

$15\%=0.15$

$\text{Bill}=\$60+\$50+0.15(\$60+\$50)$

$\text{Bill}=\$110+0.15(\$110)$

$\text{Bill}=\$110+\$16.50$

$\text{Bill}=\$126.50$

Report an Error

Example Question #12 : Fractions

Simplify: $\frac{\frac{1}{2}}{\frac{3}{4}}$

Possible Answers:

$\frac{2}{3}$

$\frac{1}{5}$

$\frac{3}{2}$

$\frac{1}{24}$

Correct answer:

$\frac{2}{3}$

Explanation:

Rewrite this complex fraction using a division sign.

$\frac{1}{2}\div\frac{3}{4}$

Take the reciprocal of the second term and change the division of the division sign. Simplify.

$\frac{1}{2}\times\frac{4}{3}=\frac{2}{3}$

Report an Error

Example Question #1 : How To Subtract Complex Fractions

Solve:

$76-\frac{75}{6}=$

Possible Answers:

$\frac{127}{2}$

$\frac{7}{6}$

$\frac{1}{6}$

Correct answer:

$\frac{127}{2}$

Explanation:

First reduce the fraction. We can divide both the numerator and the denominator by 3.

$\frac{75\div 3}{6\div 3}=\frac{25}{2}$

Now our expression looks like this:

$76-\frac{25}{2}$

When you add or subtract fractions, you need to have the same denominator. The lowest common deonminator here is 2. So we need to multiply and solve:

$\left ( \frac{2}{2}\right)\cdot76-\frac{25}{2}=\frac{152}{2}-\frac{25}{2}=\frac{127}{2}$

Report an Error

← Previous 1 2 3 4 5 6 7 8 9 … 18 19 Next →

View SAT Mathematics Tutors

Amanda
Certified Tutor

Seattle University, Current Undergrad Student, Applied Mathematics.

View SAT Mathematics Tutors

Zachary
Certified Tutor

Yale University, Bachelor of Science, Biology, General.

View SAT Mathematics Tutors

Brian
Certified Tutor

CUNY Brooklyn College, Bachelor in Arts, Economics. Hofstra University, Juris Doctor, Prelaw Studies.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

SSAT Courses & Classes in Miami, ISEE Courses & Classes in Miami, GRE Courses & Classes in Atlanta, LSAT Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in San Diego, GRE Courses & Classes in Los Angeles, GMAT Courses & Classes in Washington DC, MCAT Courses & Classes in San Diego, GRE Courses & Classes in Phoenix, SSAT Courses & Classes in Boston

Popular Test Prep

LSAT Test Prep in Phoenix, SAT Test Prep in Houston, ISEE Test Prep in Los Angeles, SSAT Test Prep in Miami, SAT Test Prep in Philadelphia, ISEE Test Prep in Miami, SSAT Test Prep in Denver, GMAT Test Prep in New York City, GMAT Test Prep in Phoenix, GRE Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : Fractions

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #11 : Fractions

Example Question #11 : How To Order Fractions From Least To Greatest Or From Greatest To Least

Example Question #13 : Fractions

Example Question #14 : Fractions

Example Question #11 : Fractions

Example Question #16 : Fractions

Example Question #17 : Fractions

Example Question #18 : Fractions

Example Question #12 : Fractions

Example Question #1 : How To Subtract Complex Fractions

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: