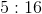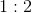For this problem, we need to find the number of employees who fall into the categories described, keeping in mind that multiple portions of the pie chart must be accommodated for. Then, we can fit them into a ratio:

For the "2 to 9 years" portion of the financial industry, include

(0.2 + 0.18)(12,000,000) = 4,560,000 workers.

For the "0 to 4 years" portion of the construction industry, include

(0.15 + 0.2)(8,000,000) = 2,800,000 workers.

Now divide and simplify to find the ratio:

4,560,000/2,800,000 = 8/5.

Since the ratios are fixed, regardless of the actual values of , , or , we can let  and

In order to convert to a form where we can relate  to , we must set the coefficient of  of each ratio equal such that the ratio can be transferred. This is done most easily by finding a common multiple of  and  (the ratio of  to  and , respectively) which is

Thus, we now have  and .

Setting the  values equal, we get , or a ratio of 

We can use dimensional analysis to solve this problem.  We will create ratios from the conversions given.

Since Joaquin cannot trade for part of a shiny rock, the most he can get is 3 shiny rocks.

First, we should write a fraction for each ratio given:

Next, we will multiply these fractions by each other in such a way that will leave us with a fraction that has only Z and M, since we want  a ration of these two flowers only.

So the final answer is 35:6

To solve for the missing value in this ratio problem, it is a two step process.

First cross-multiply:

From here, to isolate x take the opposite operation. In other words divide each side by two.

The number of hours required to mow the lawn remains constant and can be found by taking the original  workers times the  hours they worked, totaling  hours. We then split the total required hours between the  works that remain, and each of them have to work  and  hours:  .

Take the total distance travelled (600 miles) and divide it by the total time travelled (6.5 hrs + 5.5 hrs = 12 hours) = 50 miles/hour 

Call the cars “Car A” and “Car B”.

The least common multiple for the travel time of Car A and Car B is 120. We get the LCM by factoring. Car A’s travel time gives us 3 * 2 * 5; Car B’s time gives us 2 * 2 * 2 * 5.  The smallest number that accommodates all factors of both travel times is 2 * 2 * 2 * 3 * 5, or 120. There are 60 minutes in an hour, so 120 minutes equals two hours. Two hours after 1:00pm is 3:00pm.

If Jon is driving at 10 feet per second he covers 10 * 60 feet in one minute (600 ft/min). In order to determine how far he travels in thirty minutes we must multiply 10 * 60 * 30 feet in 30 minutes.

There are 60 seconds in a minute and 60 minutes in an hour, therefore 3600 seconds in an hour. The arrow will travel 3600x10= 36,000 meters in an hour.