All SAT II Math I Resources
Example Questions
Example Question #41 : Geometry
In triangle 


Which of the following statements is true about the lengths of the sides of 
In a triangle, the shortest side is opposite the angle of least measure; the longest side is opposite the angle of greatest measure. Therefore, if we order the angles, we can order their opposite sides similarly.
Since the measures of the three interior angles of a triangle must total 






Example Question #1 : Finding Sides
Which of the following describes a triangle with sides one kilometer, 100 meters, and 100 meters?
The triangle is acute and isosceles, but not equilateral.
The triangle is obtuse and isosceles, but not equilateral.
The triangle is acute and equilateral.
The triangle cannot exist.
The triangle is obtuse and scalene.
The triangle cannot exist.
One kilometer is equal to 1,000 meters, so the triangle has sides of length 100, 100, and 1,000. However,
That is, the sum of the least two sidelengths is not greater than the third. This violates the Triangle Inequality, and this triangle cannot exist.
Example Question #3 : Finding Sides

Note: Figure NOT drawn to scale.
Refer to the above diagram. Evaluate 
The correct answer is not among the other responses.
The correct answer is not among the other responses.
The altitude perpendicular to the hypotenuse of a right triangle divides that triangle into two smaller triangles similar to each other and the large triangle. Therefore, the sides are in proportion. The hypotenuse of the triangle is equal to
Therefore, we can set up, and solve for 
This is not one of the choices.
Example Question #42 : 2 Dimensional Geometry
What is the sum of three sides of a square if the fourth side has a length of 
All of the sides of a square have the same length.
That means all four sides of this square have a length of 
The sum of three of them would then be

Example Question #1 : How To Find The Length Of The Diagonal Of A Kite
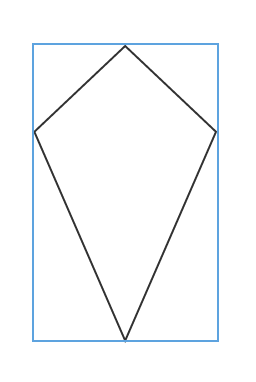
The area of the rectangle is 
The area of a kite is half the product of the diagonals.
The diagonals of the kite are the height and width of the rectangle it is superimposed in, and we know that because the area of a rectangle is base times height.
Therefore our equation becomes:

We also know the area of the rectangle is 
Thus,, the area of the kite is 
Example Question #1 : Kites

Using the kite shown above, find the length of the red (vertical) diagonal.
In order to solve this problem, first observe that the red diagonal line divides the kite into two triangles that each have side lengths of 



The solution is:
Example Question #3 : How To Find The Length Of The Diagonal Of A Kite
A kite has two perpendicular interior diagonals. One diagonal has a measurement of 

This problem can be solved by applying the area formula:
Since this question provides the area of the kite and length of one diagonal, plug that information into the equation to solve for the missing diagonal.
Thus the solution is:
Example Question #1 : How To Find The Length Of The Diagonal Of A Kite
A kite has two perpendicular interior diagonals. One diagonal has a measurement of 

You must find the length of the missing diagonal before you can find the sum of the two perpendicular diagonals.
To find the missing diagonal, apply the area formula:
This question provides the area of the kite and length of one diagonal, plug that information into the equation to solve for the missing diagonal.
Therefore, the sum of the two diagonals is:
Example Question #21 : Quadrilaterals

The area of the kite shown above is 

To find the length of the black diagonal apply the area formula:
Since this question provides the area of the kite and length of one diagonal, plug that information into the equation to solve for the missing diagonal.
Thus the solution is:
Example Question #1 : How To Find The Length Of The Diagonal Of A Trapezoid
What is the length of the diagonals of trapezoid 

To find the length of the diagonal, we need to use the Pythagorean Theorem. Therefore, we need to sketch the following triangle within trapezoid 

We know that the base of the triangle has length 
Dividing by two, we have the length of each additional side on the bottom of the trapezoid:
Adding these two values together, we get 
The formula for the length of diagonal 




Plugging in our values, we get:
Certified Tutor
All SAT II Math I Resources


















































































