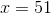The perimeter of the regular pentagon is 80, so each side measures one fifth of this, or 16. Also, each interior angle of a regular pentagon measures .

The pentagon, along with diagonal , is shown below:

A triangle  is formed with , and included angle measure . The length of the remaining side can be calculated using the law of cosines: 

,

where  and  are the lengths of two sides,  the measure of their included angle, and  the length of the side opposite that angle.

Setting , and , substitute and evaluate :

Taking the square root of both sides:

,

the correct choice.

A rhombus is a quadrilateral with four sides of equal length. Rhombuses have diagonals that bisect each other at right angles.

Thus, we can consider the right triangle  to find the length of diagonal . From the given information, each of the sides of the rhombus measures  meters and .

Because the diagonals bisect each other, we know:

Using the Pythagorean theorem,

There are twelve numbers on a clock; from one to the next, a hand rotates . At 4:45, the minute hand is exactly on the "9" - that is, at the . The hour hand is three-fourths of the way from the "4" to the "5" - that is, on the  position. Therefore, the difference is the angle they make:

There are twelve numbers on a clock; from one to the next, a hand rotates . At 8:50, the minute hand is exactly on the "10" - that is, on the  position. The hour hand is five-sixth of the way from the "8" to the "9" - that is, on the  position. Therefore, the difference is the angle they make:

.

Two of the angles of the quadrilateral formed are angles of a regular hexagon, so each measures

.

The four angles of the quadrilateral are . Their sum is , so we can set up, and solve for  in, the equation:

A triangle's angles must add up to  degrees.  

The angles given add up to 181,

.  

That means that this cannot be an actual triangle.

Step 1: Recall the sum of the angles of a triangle...

The sum of the internal angles of a triangle is .

Step 2: To find the missing angle, subtract the given angles from ...

One yard is equal to 3 feet; it is also equal to 36 inches. Therefore:

18 feet is equal to  yards, 

and

216 feet is equal to  yards.

The three sides are congruent, making the triangle equilateral - and all equilateral triangles are acute.

You can find the length of c by first finding the length of the hypotenuse of the larger similar triangle and then setting up a ratio to find the hypotenuse of the smaller similar triangle. 

You also could have found 10 by recognizing this triangle is a form of a 3-4-5 triangle. 

The hypotenuse of the bigger triangle is 10 inches.

Now that we know the length of the hypotenuse for the larger triangle, we can set up a ratio equation to find the hypotenuse of the smaller triangle. 

cross multiply

Read the question carefully and notice that the image is deceptive: these lines are not parallel. So we cannot apply any of our rules about parallel lines. So we cannot infer II or III, those are only true if the lines are parallel. If we sketch line 2 and line 3 meeting we will form a triangle and it is possible to make a = e. One such solution is to make a and e 60 degrees.