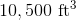Try sketching it out.

Start with one circle and then keep adding circles like a venn diagram and start counting. A region is any portion of the figure that can be defined and has a boundary with another portion. Don't forget that the exterior (labeled 14) is a region that does not have exterior boundaries.

Notice that the figure may not be to scale, and points  and  could lie anywhere on line segments  and  respectively.

Next, recall the formula for the area of a triangle:

To find the minimum area we need the smallest possible values for  and .

To make  smaller we can shift points  and  all the way to point . This will make triangle  have a height of :

 is the minimum possible value for the area.

To find the maximum value we need the largest possible values for  and . If we shift point  all the way to point  then the base of the triangle is  and the height is , which we can plug into the formula for the area of a triangle:

which is the maximum possible area of triangle 

One foot is equal to 12 inches, so the triangle would have sides 10, 12, and 24 inches. Since 

,

the triangle violates the Triangle Inequality, which states that the sum of the lengths of the two smaller sides must exceed the length of the third. The triangle cannot exist.

Nine yards is equal to  inches.

30 feet is equal to  inches.

In terms of inches, the triangle has sides of length 324, 360, 360; this exists since

and this is an isosceles triangle, since two sides have the same length.

Also,

,

making the triangle acute.

Collinear points are points that are contained in the same line. Of the four choices, only  fit the description, since all are on Line .

 gives us the congruence of two corresponding angles and one corresponding side;  this is not enough to establish similarity.

The perimeters of the triangles are irrelevant to their similarity, so  and  having the same perimeter does not help to establish similarity, with or without what is given.

 establishes the proportionality of two nonincluded sides of the angles known to be congruent. However, there is no statement that establishes similarity as a result of this.

, along with , sets up the conditions of the Angle-Angle Similarity Postulate, which states that if two triangles have two pairs of congruent angles between them, the triangles are similar.  is the correct choice.

Below is the regular Octagon , with the referenced midpoint  and segment . Note that perpendiculars have also been constructed from  and  to meet  at  and , respectively.

 is a right triangle with legs  and  and hypotenuse .

The perimeter of the regular octagon is 80, so the length of each side is one-eighth of 80, or 10. Consequently,

To find the length of , we can break it down as

Quadrilateral  is a rectangle, so .

 is a 45-45-90 triangle with leg  and hypotenuse ; by the 45-45-90 Triangle Theorem, 

For similar reasons, .

Therefore,

 can now be evaluated using the Pythagorean Theorem:

Substituting and evaluating:

,

the correct choice.

The pool can be seen as a cylinder with diameter  - and, subsequently, radius half this, or  - and depth, or height, 2. The volume of a cylinder is defined by the formula

The cross-section of the pool is the area of its surface, which is the product of its length and its width:

 square feet.

Since 60% of the pool is six feet deep, this portion of the pool holds 

 cubic feet of water.

Since the remainder of the pool - 40% - is four feet deep, this portion of the pool holds 

 cubic feet of water.

Add them together: the pool holds 

 cubic feet of water.

This answer is not among the choices.

Convert the side dimension to inches first before finding the volume.

Write the volume for a cube and substitute the new side to obtain the volume in inches.