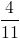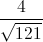Call Now to Set Up Tutoring:

(888) 888-0446

PSAT Math : PSAT Mathematics

Study concepts, example questions & explanations for PSAT Math

Create An Account

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #83 : Basic Squaring / Square Roots

If m and n are postive integers and 4^m = 2ⁿ, what is the value of m/n?

Possible Answers:

1/2

Correct answer:

1/2

Explanation:

2²= 4. Also, following the rules of exponents, 4¹= 1.
One can therefore say that m = 1 and n = 2.
The question asks to solve for m/n. Since m = 1 and n = 2, m/n = 1/2.

Report an Error

Example Question #1751 : Psat Mathematics

Simplify the radical:

$\sqrt{320}$

Possible Answers:

$8\sqrt{20}$

$\sqrt{320}$

$8\sqrt{5}$

$4\sqrt{5}$

$4\sqrt{20}$

Correct answer:

$8\sqrt{5}$

Explanation:

$\sqrt{320}=\sqrt{2\times 160}=\sqrt{2\times 2\times 80}=2\sqrt{80}=2\sqrt{2\times 40}=2\sqrt{2\times 2\times 20}=2\times 2\times \sqrt{20}=4\sqrt{2\times 10}=4\sqrt{2\times 2\times 5}=4\times 2\times \sqrt{5}=8\sqrt{5}$

Report an Error

Example Question #14 : Square Roots And Operations

Simplify.

$\sqrt{\frac{16}{121}}$

Possible Answers:

$\frac{4}{11}$

$\frac{4}{\sqrt{121}}$

$16\sqrt{121}$

$\frac{8}{61}$

$\frac{16}{121}$

Correct answer:

$\frac{4}{11}$

Explanation:

$\sqrt{\frac{16}{121}}$

Take the square root of both the top and bottom terms.

$\frac{\sqrt{16}}{\sqrt{121}}$

Simplify.

$\frac{4}{11}$

Report an Error

Example Question #1 : Other Squaring / Square Roots

The square root of 5184 is:

Possible Answers:

Correct answer:

Explanation:

The easiest way to narrow down a square root from a list is to look at the last number on the squared number – in this case 4 – and compare it to the last number of the answer.

70 * 70 will equal XXX0

71 * 71 will equal XXX1

72 * 72 will equal XXX4

73 * 73 will equal XXX9

74 * 74 will equal XXX(1)6

Therefore 72 is the answer. Check by multiplying it out.

Report an Error

Example Question #2 : Other Squaring / Square Roots

If $5^{x}+5^{x}+5^{x}+5^{x}+5^{x}=5^{10}$ , what is the value of x?

Possible Answers:

Correct answer:

Explanation:

$5(5^{x})=5^{10}$

$5^{1}(5^{x})=5^{10}$

$5^{x+1}=5^{10}$

$x=9$

Report an Error

Example Question #3 : Other Squaring / Square Roots

If x and y are integers and xy + y² is even, which of the following statements must be true?

I. 3y is odd

II. y/2 is an integer

III. x^y is even

Possible Answers:

$None\ of\ the\ statements\ must\ be\ true$

I & II

II only

I only

I, II, & III

Correct answer:

$None\ of\ the\ statements\ must\ be\ true$

Explanation:

In order for the original statement to be true, the and $y^{2}$ terms must be either both odd or both even. Looking at each of the statements individually,

I. States that is odd, but only odd values multiplied by 3 are odd. If was an even number, the result would be even. But can be either odd or even, depending on what equals. Thus this statement COULD be true but does not HAVE to be true.

II. States that $\frac{y}{2}$ is an integer, and since only even numbers are cleanly divided by 2 (odd values result in a fraction) this ensures that is even. However, can also be odd, so this is a statement that COULD be true but does not HAVE to be true.

III. For exponents, only the base value determines whether it is even or odd - it does not indicate the value of y at all. Only even numbers raised to any power are even, thus, this ensures that is even. But can be odd as well, so this statement COULD be true but does not HAVE to be true.

An example of two integers that will work violate conditions II and III is x=1 and y=3 .

$(1)\cdot (3)+(3)^{2}=3+9=12$ , and even number.

$\frac{3}{2}$ is not an integer.

$1^{3}=1$ is not even.

Furthermore, any combination of 2 even integers will make the original statement true, and violate the Statement I.

Report an Error

Example Question #4 : Other Squaring / Square Roots

How many integers from 20 to 80, inclusive, are NOT the square of another integer?

Possible Answers:

Correct answer:

Explanation:

First list all the integers between 20 and 80 that are squares of another integer:

5² = 25

6² = 36

7²= 49

8² = 64

In total, there are 61 integers from 20 to 80, inclusive. 61 – 4 = 57

Report an Error

Example Question #5 : How To Find The Square Of An Integer

Let the universal set be the set of all positive integers.

Let be the set of all multiples of 3; let be the set of all multiples of 7; let be the set of all perfect square integers. Which of the following statements is true of 243?

Note: means "the complement of ", etc.

Possible Answers:

$243 \in A \cap B \cap C$

$243 \in A \cap B' \cap C$

$243 \in A' \cap B \cap C'$

$243 \in A \cap B' \cap C'$

$243 \in A' \cap B \cap C$

Correct answer:

$243 \in A \cap B' \cap C'$

Explanation:

$243 \div 3 = 81$ , so 243 is divisible by 3. $243 \in A$ .

$243 \div 7= 34 \textup{ R }5$ , so 243 is not divisible by 7. $243 \notin B$ - that is, $243 \in B'$ .

$15 = \sqrt{225}< \sqrt{243} < \sqrt{256} = 16$ , 243 is not a perfect square integer. $243 \notin C$ - that is, $243 \in C'$ .

Since 243 is an element of , , and , it is an element of their intersection. The correct choice is that

$243 \in A \cap B' \cap C'$

Report an Error

Example Question #5 : How To Find The Square Of An Integer

Consider the inequality:

$x< x^{5}< x^{4}$

Which of the following could be a value of ?

Possible Answers:

$x=-\frac{3}{4}$

$x=-\frac{4}{3}$

$x=-1$

There is no possible value for $x$

$x=1$

Correct answer:

$x=-\frac{3}{4}$

Explanation:

Notice how $x^4$ is the greatest value. This often means that $x$ is negative as $(-1)^n=-1$ when $\dpi{100} n$ is odd and $(-1)^n=1$ when $\dpi{100} n$ is even.

Let us examine the first choice, $x=-\frac{3}{4}$

$x^5=-\frac{3^5}{4^5}=-\frac{243}{1024}> -\frac{3}{4}$

This can only be true of a negative value that lies between zero and one.

Report an Error

Example Question #2 : How To Find The Square Of An Integer

$\sqrt{y^2-63}=9$

In the equation above, if is a positive integer, what is the value of ?

Possible Answers:

Correct answer:

Explanation:

Begin by squaring both sides of the equation:

$\sqrt{y^2-63}=9$

$(\sqrt{y^2-63})^2=9^2$

y^2-63=81

Now solve for y:

y^2-63+63=81+63

y^2=144

y=12

Note that must be positive as defined in the original question. In this case, must be 12.

Report an Error

View PSAT Mathematics Tutors

Eva
Certified Tutor

Technicka Univerzita Liberec, Bachelor of Education, Education.

View PSAT Mathematics Tutors

Leonard
Certified Tutor

Florida State University, Bachelor of Science, Environmental Science.

View PSAT Mathematics Tutors

Rodolfo
Certified Tutor

The University of Texas at San Antonio, Bachelor of Science, Mathematics.

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GRE Tutors in Washington DC, GMAT Tutors in Miami, ACT Tutors in Miami, ACT Tutors in New York City, SAT Tutors in San Diego, Algebra Tutors in Denver, Algebra Tutors in Atlanta, Biology Tutors in Philadelphia, GMAT Tutors in Denver, SSAT Tutors in Atlanta

Popular Courses & Classes

GRE Courses & Classes in Phoenix, ISEE Courses & Classes in Boston, GRE Courses & Classes in Chicago, SAT Courses & Classes in Miami, GRE Courses & Classes in Philadelphia, SSAT Courses & Classes in Boston, GMAT Courses & Classes in Houston, GRE Courses & Classes in Houston, ISEE Courses & Classes in Chicago, ACT Courses & Classes in Dallas Fort Worth

Popular Test Prep

SSAT Test Prep in Atlanta, ACT Test Prep in Dallas Fort Worth, LSAT Test Prep in Houston, GMAT Test Prep in Houston, LSAT Test Prep in San Diego, MCAT Test Prep in Chicago, ACT Test Prep in Seattle, GRE Test Prep in Chicago, ACT Test Prep in Washington DC, SAT Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

PSAT Math : PSAT Mathematics

Study concepts, example questions & explanations for PSAT Math

All PSAT Math Resources

Example Questions

Example Question #83 : Basic Squaring / Square Roots

Example Question #1751 : Psat Mathematics

Example Question #14 : Square Roots And Operations

Example Question #1 : Other Squaring / Square Roots

Example Question #2 : Other Squaring / Square Roots

Example Question #3 : Other Squaring / Square Roots

Example Question #4 : Other Squaring / Square Roots

Example Question #5 : How To Find The Square Of An Integer

Example Question #5 : How To Find The Square Of An Integer

Example Question #2 : How To Find The Square Of An Integer

All PSAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: