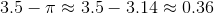Begin by solving for :

Now, this is represented by drawing an open circle at 6 and graphing upward to infinity:

First, we must find out by how much they are spaced by. It cannot be 1, since 4(4) = 16, which is too great of a step in the positive direction and exceeds the equal-spacing limit. 2 works perfectly, however, as 4(2) equals 8 and fits in line with the equal spacing.

Next, we can find the values of x and y since we are given a value of 6 for the third tick mark. As such, x (6 – 4) and y (6 – 2) are 2 and 4, respectively.

Finally, z is 4 steps away from y, and since each step has a value of 2, 2(4) = 8, plus the value that y is already at, 8 + 4 = 12 (or can simply count).

Finding the average of all 3 values, we get (2 + 4 + 12)/3 = 18/3 = 6.

The cubes of integers from 1 to 250 are 1, 8, 27,64,125,216.

, so 

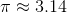
Therefore, 

On the number line,  appears between 0.3 and 0.4 and is the correct choice.

The absolute value of a negative number can be calculated by simply removing the negative symbol. Therefore,

All four (negative) numbers in the set  are less than this positive number.

Let's reductively consider what this data tells us.

Consider each group (a,b,c) as a group of signs.

From abc < 0, we know that the following are possible:

(–, +, +), (+, –, +), (+, +, –), (–, –, –)

From ab > 0, we know that we must eliminate (–, +, +) and (+, –, +)

From bc > 0, we know that we must eliminate (+, +, –)

Therefore, any of our answers must hold for (–, –, –)

This eliminates immediately a > 0, b > 0

Likewise, it eliminates a – b > 0 because we do not know the relative sizes of a and b. This could therefore be positive or negative.

Finally, ac is a product of negatives and is therefore positive. Hence ac < 0 does not hold.

We are left with a + b < 0, which is true, for two negatives added must be negative.

A negative number divided by a negative number always results in a positive number.  divided by  equals . Since the answer is positive, the answer cannot be  or any other negative number.

Begin by isolating your variable.

Subtract  from both sides:

, or 

Next, subtract  from both sides:

, or 

Then, divide both sides by :

Recall that division of a negative by a negative gives you a positive, therefore:

 or 

Because is positive,  must be negative since the product of two negative numbers is positive.

Because  is also positive, must also be negative in order to produce a prositive product.

To check you answer, you can try plugging in any negative number for .

A negative integer raised to an integer power is positive if and only if the absolute value of the exponent is even. Since the sum or difference of two odd integers is always an even integer, this is the case in all three expressions. The correct response is all of these.