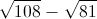Call Now to Set Up Tutoring:

(888) 888-0446

PSAT Math : PSAT Mathematics

Study concepts, example questions & explanations for PSAT Math

Create An Account

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Basic Squaring / Square Roots

Divide and simplify. Assume all integers are positive real numbers.

$\sqrt{\frac{32}{4}}$

Possible Answers:

$\sqrt{2}$

$4\sqrt{2}$

$\sqrt{8}$

$2\sqrt{2}$

Correct answer:

$2\sqrt{2}$

Explanation:

$\sqrt{\frac{32}{4}}$

There are two ways to solve this problem. First you can divide the numbers under the radical. Then simplify.

Example 1

$\sqrt{\frac{32}{4}}=\sqrt{8}=\sqrt{4}\cdot\sqrt{2}=2\sqrt{2}$

Example 2

Find the square root of both numerator and denominator, simplifying as much as possible then dividing out like terms.

$\sqrt{\frac{32}{4}}=\frac{\sqrt{32}}{\sqrt{4}}=\frac{\sqrt{16}\cdot \sqrt{2}}{\sqrt{4}}=\frac{4\sqrt{2}}{2}=2\sqrt{2}$

Both methods will give you the correct answer of $2\sqrt{2}$ .

Report an Error

Example Question #1 : Basic Squaring / Square Roots

(√27 + √12) / √3 is equal to

Possible Answers:

5/√3

√3

(6√3)/√3

Correct answer:

Explanation:

√27 is the same as 3√3, while √12 is the same as 2√3.

3√3 + 2√3 = 5√3

(5√3)/(√3) = 5

Report an Error

Example Question #1731 : Psat Mathematics

Simplify:

$\sqrt{\frac{64}{169}}$

Possible Answers:

$\frac{7}{13}$

$\frac{8}{13}$

$\frac{8}{15}$

$\frac{64}{169}$

Correct answer:

$\frac{8}{13}$

Explanation:

To simplfy, we must first distribute the square root.

$\frac{\sqrt{64}}{\sqrt{169}}$

Next, we can simplify each of the square roots.

$\frac{8}{13}$

Report an Error

Example Question #3 : Basic Squaring / Square Roots

Find the quotient:

$\sqrt{\frac{18}{2}}$

Possible Answers:

$\frac{\sqrt{2}}{3}$

$\frac{3\sqrt{2}}{2}$

$\sqrt{2}$

Correct answer:

Explanation:

Find the quotient:

$\frac{\sqrt{18}}{\sqrt{2}}$

There are two ways to approach this problem.

Option 1: Combine the radicals first, the reduce

$\frac{\sqrt{18}}{\sqrt{2}}=\sqrt{\frac{18}{2}}=\sqrt{9}=3$

Option 2: Simplify the radicals first, then reduce

$\frac{\sqrt{18}}{\sqrt{2}}=\frac{\sqrt{9\cdot 2}}{\sqrt{2}}=\frac{3\sqrt{2}}{\sqrt{2}}=3$

Report an Error

Example Question #1 : Square Roots And Operations

Find the quotient:

$\frac{\sqrt{54}}{\sqrt{45}}$

Possible Answers:

$\frac{\sqrt{30}}{5}$

$9\sqrt{5}$

$3\sqrt{6}$

$\frac{\sqrt{}6}{\sqrt{}5}$

Correct answer:

$\frac{\sqrt{30}}{5}$

Explanation:

Simplify each radical:

$\frac{\sqrt{54}}{\sqrt{45}} = \frac{\sqrt{9\cdot 6}}{\sqrt{9\cdot 5}}=\frac{3\sqrt{6}}{3\sqrt{5}}=\frac{\sqrt{6}}{\sqrt{5}}$

Rationalize the denominator:

$\frac{\sqrt{6}}{\sqrt{5}} \cdot \frac{\sqrt{5}}{\sqrt{5}}= \frac{\sqrt{30}}{5}$

Report an Error

Example Question #171 : Arithmetic

Evaluate: $\sqrt{108}-\sqrt{81}$

Possible Answers:

None of the available answers

$24\sqrt{3}-81$

$24\sqrt{3}-9$

$4\sqrt{27}-\sqrt{9}$

$6\sqrt{3}-9$

Correct answer:

$6\sqrt{3}-9$

Explanation:

Let us factor 108 and 81

$108=2\times 54= 2\times 2\times 27= 2^2\times 3\times 9= 2^2\times 3^2\times 3$

$81=9\times 9=9^2$

$\sqrt{108}-\sqrt{81}=6\sqrt{3}-9$

Report an Error

Example Question #1 : How To Subtract Square Roots

$\sqrt{63}-\sqrt{28}$

Possible Answers:

$5\sqrt{7}$

$3\sqrt{11}$

$\sqrt{5}$

$\sqrt{35}$

$\sqrt{7}$

Correct answer:

$\sqrt{7}$

Explanation:

Step one: Find the greatest square factor of each radical

For this is , and for it is .

Therefore:

$\sqrt{63}-\sqrt{28}=\sqrt{9*7}-\sqrt{4*7}$

Step two: Simplify the radicals

$\sqrt{9*7}-\sqrt{4*7}$

$3\sqrt{7}-2\sqrt{7}$

$\sqrt{7}$

Report an Error

Example Question #1 : Basic Squaring / Square Roots

Simplify.

$\sqrt{32}+\sqrt{64}+\sqrt{8}$

Possible Answers:

$28\sqrt{2}$

$6\sqrt{2}+8$

$12\sqrt{2}+8$

$16\sqrt{2}+8$

Correct answer:

$6\sqrt{2}+8$

Explanation:

$\sqrt{32}+\sqrt{64}+\sqrt{8}$

First step is to find perfect squares in all of our radicans.

$\sqrt{32}\rightarrow\sqrt{16\cdot 2}\rightarrow4\sqrt{2}$

$\sqrt{64}\rightarrow\sqrt{8\cdot 8}\rightarrow8$

$\sqrt{8}\rightarrow\sqrt{4\cdot 2}\rightarrow2\sqrt{2}$

After doing so you are left with $4\sqrt{2}+2\sqrt{2}+8$

*Just like fractions you can only add together coefficents with like terms under the radical. *

$6\sqrt{2}+8$

Report an Error

Example Question #21 : Basic Squaring / Square Roots

If $\sqrt{x}=3^2$ what is $x$ ?

Possible Answers:

$729$

$3$

$9$

$27$

$81$

Correct answer:

$81$

Explanation:

Square both sides:

x = (3²)²= 9² = 81

Report an Error

Example Question #7 : Basic Squaring / Square Roots

Simplify:

$\sqrt{27}-\sqrt{48}+\sqrt{81}$

Possible Answers:

$-\sqrt{3}+9$

$7\sqrt{3}+9$

$2\sqrt{3}$

$\sqrt{63}$

Correct answer:

$-\sqrt{3}+9$

Explanation:

To combine radicals, they must have the same radicand. Therefore, we must find the perfect squares in each of our square roots and pull them out.

$\sqrt{27}\rightarrow \sqrt{9*3}\rightarrow \sqrt{3^2*3}\rightarrow 3\sqrt{3}$

$\sqrt{48}\rightarrow \sqrt{16*3}\rightarrow \sqrt{4^2*3}\rightarrow 4\sqrt{3}$

$\sqrt{81}\rightarrow\sqrt{9*9}\rightarrow\sqrt{9^2}\rightarrow9$

Now, we plug these equivalent expressions back into our equation and simplify:

$\sqrt{27}-\sqrt{48}+\sqrt{81}$

$3\sqrt3-4\sqrt3+9$

$-\sqrt3+9$

Report an Error

View PSAT Mathematics Tutors

Yasmin
Certified Tutor

Johns Hopkins University, Bachelor in Arts, Mathematics.

View PSAT Mathematics Tutors

Melinda
Certified Tutor

University of North Carolina at Chapel Hill, Bachelor in Arts, French Studies. University of Maryland-College Park, Master of...

View PSAT Mathematics Tutors

Omar
Certified Tutor

Arizona State University, Bachelors, Civil Engineering.

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Algebra Tutors in Washington DC, Computer Science Tutors in New York City, Chemistry Tutors in Atlanta, Reading Tutors in Dallas Fort Worth, SSAT Tutors in Houston, Algebra Tutors in Houston, LSAT Tutors in Boston, MCAT Tutors in Denver, Reading Tutors in Chicago, Spanish Tutors in Atlanta

Popular Courses & Classes

MCAT Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Washington DC, GMAT Courses & Classes in Seattle, ACT Courses & Classes in Houston, ISEE Courses & Classes in Phoenix, LSAT Courses & Classes in Denver, SSAT Courses & Classes in Houston, LSAT Courses & Classes in San Diego, ISEE Courses & Classes in San Diego, GRE Courses & Classes in Phoenix

Popular Test Prep

ISEE Test Prep in Washington DC, GMAT Test Prep in Seattle, ISEE Test Prep in San Francisco-Bay Area, GRE Test Prep in Phoenix, ISEE Test Prep in Phoenix, GMAT Test Prep in Washington DC, SSAT Test Prep in Houston, GRE Test Prep in New York City, GRE Test Prep in Chicago, SSAT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

PSAT Math : PSAT Mathematics

Study concepts, example questions & explanations for PSAT Math

All PSAT Math Resources

Example Questions

Example Question #1 : Basic Squaring / Square Roots

Example Question #1 : Basic Squaring / Square Roots

Example Question #1731 : Psat Mathematics

Example Question #3 : Basic Squaring / Square Roots

Example Question #1 : Square Roots And Operations

Example Question #171 : Arithmetic

Example Question #1 : How To Subtract Square Roots

Example Question #1 : Basic Squaring / Square Roots

Example Question #21 : Basic Squaring / Square Roots

Example Question #7 : Basic Squaring / Square Roots

All PSAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: