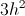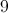All PSAT Math Resources
Example Questions
Example Question #11 : How To Find The Length Of The Side Of An Acute / Obtuse Triangle
All of the following could be the possible side lengths of a triangle EXCEPT:
The length of the third side of a triangle must always be between (but not equal to) the sum and the difference of the other two sides.
For instance, take the example of 2, 6, and 7.


The 5, 7, 12 answer choice is the only option for which this is not the case.


Example Question #1 : How To Find If Two Acute / Obtuse Triangles Are Similar


The perimeter is equal to the sum of the three sides. In similar triangles, each side is in proportion to its correlating side. The perimeters are also in equal proportion.
Perimeter A = 45” and perimeter B = 135”
The proportion of Perimeter A to Perimeter B is 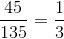
This applies to the sides of the triangle. Therefore to get the any side of Triangle B, just multiply the correlating side by 3.
15” x 3 = 45”
10” x 3 = 30“

Example Question #1 : How To Find The Height Of An Acute / Obtuse Triangle
Find the height of a triangle if the area of the triangle = 18 and the base = 4.
9
4
1
6
9
The area of a triangle = (1/2)bh where b is base and h is height. 18 = (1/2)4h which gives us 36 = 4h so h =9.
Example Question #31 : Acute / Obtuse Triangles
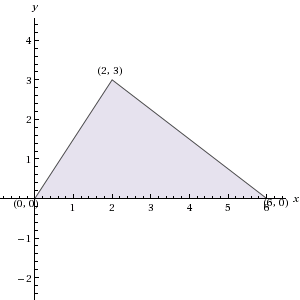
If triangle ABC has vertices (0, 0), (6, 0), and (2, 3) in the xy-plane, what is the area of ABC?
9
12
20
10
18
Example Question #1 : How To Find The Area Of An Acute / Obtuse Triangle
The height, 



If 


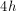
Using the formula for the area of a triangle (


Example Question #12 : Geometry
How many diagonals are there in a regular hexagon?
A diagonal is a line segment joining two non-adjacent vertices of a polygon. A regular hexagon has six sides and six vertices. One vertex has three diagonals, so a hexagon would have three diagonals times six vertices, or 18 diagonals. Divide this number by 2 to account for duplicate diagonals between two vertices. The formula for the number of vertices in a polygon is:
where 
Example Question #13 : Geometry
How many diagonals are there in a regular hexagon?
6
3
10
18
9
9
A diagonal connects two non-consecutive vertices of a polygon. A hexagon has six sides. There are 3 diagonals from a single vertex, and there are 6 vertices on a hexagon, which suggests there would be 18 diagonals in a hexagon. However, we must divide by two as half of the diagonals are common to the same vertices. Thus there are 9 unique diagonals in a hexagon. The formula for the number of diagonals of a polygon is:
where n = the number of sides in the polygon.
Thus a pentagon thas 5 diagonals. An octagon has 20 diagonals.
Example Question #1 : How To Find The Length Of The Diagonal Of A Hexagon
Regular Hexagon 

Give the length of diagonal 
The key is to examine 

Each interior angle of a regular hexagon, including 




Also, by symmetry,

so 
and 



By the 




Example Question #571 : Geometry
Regular Hexagon 

Give the length of diagonal 
The key is to examine 

Each interior angle of a regular hexagon, including 




Also, by symmetry,

so 
and 



By the 





Example Question #1 : How To Find The Length Of The Diagonal Of A Hexagon
Regular hexagon 
Give the length of diagonal 
The key is to examine 

Each interior angle of a regular hexagon, including 





Also, by symmetry,

so 
Therefore, 



The hypotenuse 



Certified Tutor
All PSAT Math Resources