Angle Bisector Theorem

Theorems can be very useful to us in the world of mathematics. A theorem is something that we know is true -- something that can be proven. In simpler terms, theorems are tricks that we can use to solve all kinds of math problems. One such theorem is the angle bisector theorem. Let's find out how it works:

The angle bisector theorem, explained

Before we get into the angle bisector theorem, we need to review an important term:

• Angle Bisector: An angle bisector is a line that goes through an angle, dividing it into two equal angles. If this angle exists inside a shape, then the angle bisector goes through a vertex.

So what exactly is the angle bisector theorem? The theorem states that:

• An angle bisector in a triangle divides the opposite side into two segments. These two segments are divided in such a way that they are proportionate to the other two sides of the triangle.

Remember that if two things are proportionate, it means that they have equivalent ratios or fractions. For example, 1:2 and 5:10 are equivalent.

For example, if an angle bisector divides the opposite side into two segments that are 5 cm and 3 cm, this would result in a ratio of 5:3. This would also mean that the other two sides of the triangle must be proportionate to this ratio -- perhaps 10:6.

Note that different textbooks may use slightly different definitions when referring to the angle bisector theorem, but the following definition is the most common.

Visualizing the angle bisector theorem

As always, it helps to visualize this theorem in action in order to fully understand it:

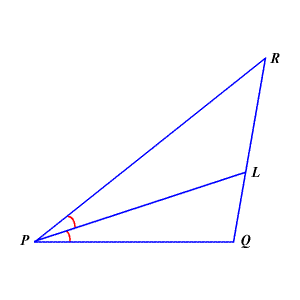
As we can see, the angle P has been divided by an angle bisector. This bisector continues and intersects with line RQ at point L.

If we were to write the angle bisector theorem in a formula based on the above diagram, we would get something like this:

If line PL bisects ∠RPQ, then $\frac{\mathrm{RL}}{\mathrm{LQ}}=\frac{\mathrm{PR}}{\mathrm{PQ}}$

Proving the angle bisector theorem

As you might recall, all theorems can be proven. This is how we know we can rely on them. So can we prove that the angle bisector theorem is correct? Let's try:

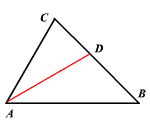
Based on the above triangle, we can safely say that:

$\frac{\mathrm{BD}}{\mathrm{DC}}=\frac{\mathrm{AB}}{\mathrm{AC}}$

But can we prove it?

Let's start by drawing a new line, creating an entirely new triangle underneath the first triangle:

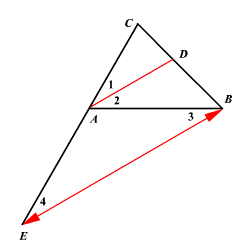
Why did we do this? As we can see, there are now two parallel lines: BE and AD.

This parallelism allows us to apply the side-splitter theorem. This theorem states that:

$\frac{\mathrm{CD}}{\mathrm{DB}}=\frac{\mathrm{CA}}{\mathrm{AE}}$

We also know that angles 1 and 4 are corresponding, which means that they must be congruent. In other words, they have the same angle measure.

Based on the fact that AD is the angle bisector of $\angle \mathrm{CAB}$ , we also know that $\angle 1$ is congruent to $\angle 2$ .

Now we can apply the alternate interior angle theorem, which states that $\angle 2$ is congruent to $\angle 3$ .

Finally, we apply the transitive property, which states that $\angle 4$ is congruent to $\angle 3$ .

What does this all mean? We have just established that $∆\mathrm{ABE}$ is an isosceles triangle with two equal sides: AE and AB.

Now we can replace AE with AB and solve our previous equation:

$\frac{\mathrm{CD}}{\mathrm{DB}}=\frac{\mathrm{CA}}{\mathrm{AB}}$

Therefore, the angle bisector theorem is proven true.

Using the angle bisector theorem

Consider the following triangle:

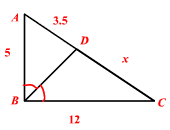
Can we use this information to find the value of x?

Let's start with our formula for the angle bisector theorem:

$\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{AD}}{\mathrm{DC}}$

Now let's plug in our values:

$\frac{5}{12}=\frac{3.5}{x}$

With a little cross-multiplication, we get:

$5x=42$

$x=8.4$

Topics related to the Angle Bisector Theorem

Triangles

Angle Bisector

Congruent Angles

Flashcards covering the Angle Bisector Theorem

Advanced Geometry Flashcards

Common Core: High School - Geometry Flashcards

Practice tests covering the Angle Bisector Theorem

Common Core: High School - Geometry Diagnostic Tests

Advanced Geometry Diagnostic Tests

Pair your student with a tutor who understand the angle bisector theorem

Aside from the angle bisector theorem, there are many others to keep track of. This isn't always easy for the average student, and a tutor can help them memorize theorems with a number of helpful tips and tricks. They can also personalize their methods based on your student's learning style. For example, visual learners can memorize theorems using flashcards. Tutoring can be helpful for students of all ability levels, so let Varsity Tutors pair your student with an appropriate tutor today.