Simplificando expresiones con radicales
Antes de que podamos simplificar una expresión radical, debemos conocer las importantes propiedades de los radicales.
PROPIEDAD DEL PRODUCTO DE LAS RAÍCES CUADRADAS
Para todos los números reales a y b ,

Esto es, la raíz cuadrada del producto es lo mismo que el producto de las raíces cuadradas.
Hay también una propiedad del cociente análoga:
Para todos los números reales a y b , b ≠ 0:

SIMPLIFICANDO RADICALES
La idea aquí es encontrar un factor de cuadrado perfecto del radicando, escribir el radicando como un producto, y luego usar la propiedad del producto para simplificar.
Ejemplo 1:
Simplifique.

9 es un cuadrado perfecto, que también es un factor de 45.

Use la propiedad del producto.


Si el número bajo el radical no tiene factores de cuadrado perfecto, entonces no puede simplificarse más. Por ejemplo
 no puede simplificarse más porque los únicos factores de 17 son 17 y 1. Así, no tiene otros factores de cuadrado perfecto más que 1.
no puede simplificarse más porque los únicos factores de 17 son 17 y 1. Así, no tiene otros factores de cuadrado perfecto más que 1.
Ejemplo 2:
Simplifique.

Use la propiedad del cociente para escribir debajo de un signo sencillo de raíz cuadrada.

Divida.

Una expresión es considerada simplificada solo si no hay signo de radical en el denominador. Si tenemos un signo radical, tenemos que racionalizar el denominador . Esto se logra al multiplicar tanto el numerador como el denominador por el radical en el denominador. Dese cuenta aquí, que solamente estamos multiplicando por una forma especial de 1, así que no cambia el valor de la expresión.
Ejemplo 3:
Simplifique.


Simplifique.

Algunas veces necesitamos usar una combinación de pasos.
Ejemplo 4:
Simplifique.
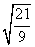
21 y 9 tienen un factor común de 3, así reduzca la fracción bajo el radical.

Ahora racionalice el denominador.

Solamente podemos sumar o restar dos expresiones radicales si los radicandos son iguales. Por ejemplo,
 no puede simplificarse más. Pero podemos simplificar
no puede simplificarse más. Pero podemos simplificar
 al usar la
propiedad distributiva
, porque los radicandos son iguales.
al usar la
propiedad distributiva
, porque los radicandos son iguales.

Tenga cuidado! Algunas ocasiones, los radicandos se ven diferentes, pero es posible simplificar y obtener el mismo radicando.
Ejemplo 5:
Simplifique.

Simplifique ambos radicales:
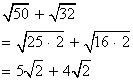
Ahora, los radicandos son iguales. Sume uitilizando la propiedad distributiva.

- SHSAT Test Prep
- CRM - Certified Risk Manager Courses & Classes
- TypeScript Tutors
- Delaware Bar Exam Test Prep
- College Math Tutors
- Math Tutors
- SPPA - Senior Professional Public Adjuster Test Prep
- Macrosociology Tutors
- Cardiology Tutors
- ARDMS - American Registry for Diagnostic Medical Sonography Test Prep
- Reading Tutors
- SEE - Special Enrollment Exam Courses & Classes
- CRM - Certified Risk Manager Test Prep
- AP U.S. Government & Politics Tutors
- Dietician Tutors
- Texas Bar Exam Test Prep
- DAT Reading Comprehension Tutors
- Bar Exam Tutors
- Technical Writing Tutors
- Elementary Level Spanish Tutors