Operaciones en conjuntos
Recuerde que un conjunto es una colección de elementos.
Dados los conjuntos A y B , podemos definir las siguientes operaciones:
|
Operación
|
Notación
|
Significado
|
|
Intersección
|
|
todos los elementos que están tanto en
A
como en
B
|
|
Unión
|
|
todos los elementos que están ya sea en
A
o
B
(o ambos)
|
|
Diferencia
|
|
todos los elementos que están en
A
pero no en
B
|
|
Complemento
|
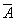(o
)
|
todos los elementos que no están en
A
|
Ejemplo 1:
Digamos que A = {1, 2, 3, 4} y digamos que B = {3, 4, 5, 6}.
Entonces:
= {3, 4}
= {1, 2, 3, 4, 5, 6}
= {1, 2}
= {todos los números reales excepto 1, 2, 3, y 4}
Ejemplo 2:
Digamos que A = { y , z } y digamos que B = { x , y , z }.
Entonces:
= {
y
,
z
}
= {
x
,
y
,
z
}
=
= {todo excepto
y
y
z
}
