We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

HiSET: Math : HiSet: High School Equivalency Test: Math

Study concepts, example questions & explanations for HiSET: Math

Create An Account

All HiSET: Math Resources

125 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Perimeter And Circumference

The area of a square is . In terms of , give the perimeter of the square.

Possible Answers:

$4 \sqrt{A }$

$2A^{2}$

$\sqrt{2A}$

$2\sqrt{A}$

$4A^{2}$

Correct answer:

$4 \sqrt{A }$

Explanation:

The length of one side of a square is equal to the square root of its area, so, if the area of a square is , the common sidelength is $\sqrt{A}$ . Since a square comprises four sides of equal length, the perimeter is equal to four times this length, or $4\sqrt{A}$ .

Report an Error

Example Question #81 : Hi Set: High School Equivalency Test: Math

The perimeter of a regular octagon is $16\sqrt{6}$ . Give the length of one side.

Possible Answers:

$2\sqrt{6}$

$4\sqrt{6}$

$8\sqrt{6}$

Correct answer:

$2\sqrt{6}$

Explanation:

A regular octagon has eight sides of equal length. Its perimeter is equal to the sum of the lengths of its sides, so the length of one side can be computed by dividing the perimeter by 8, as follows:

$l = \frac{P}{8}= \frac{16\sqrt{6}}{8} = \frac{16}{8} \sqrt{6}= 2\sqrt{6}$ ,

the correct response.

Report an Error

Example Question #82 : Hi Set: High School Equivalency Test: Math

Give the perimeter of a regular octagon in yards if the length of each side is feet.

Possible Answers:

3x+8 yards

$\frac{8}{3}x$ yards

$\frac{3}{8}x$ yards

$\frac{1}{24}x$ yards

24x yards

Correct answer:

$\frac{8}{3}x$ yards

Explanation:

The perimeter of a regular octagon - the sum of the lengths of its (eight congruent) sides - is eight times the common sidelength, so the perimeter of the octagon is feet. One yard is equivalent to three feet, so divide this by conversion factor 3 to get $\frac{8x}{3}$ yards - the correct response.

Report an Error

Example Question #1 : Perimeter And Circumference

Hexagon

Hexagon ABCDEF is regular. Give the perimeter of Trapezoid ABEF .

Possible Answers:

$9+ 3\sqrt{3}$

$9+ 3\sqrt{2}$

Correct answer:

Explanation:

A regular hexagon can be divided into six equilateral triangles, as follows:

Hexagon

The perimeter of Trapezoid ABEF can be seen to be 3+3+(3+3)+3 = 15 .

Report an Error

Example Question #1 : Arc Length And Area Of A Sector

Circle area

The depicted circle has a radius of 3 cm. The arc length between the two points shown on the circle is $\pi$ cm. Find the area of the enclosed sector (highlighted in green).

Possible Answers:

$\frac{1}{6}\; cm^2$

$27\; cm^2$

$\frac{3\pi}{2}\; cm^2$

$\frac{\pi}{6}\; cm^2$

$\pi\; cm^2$

Correct answer:

$\frac{3\pi}{2}\; cm^2$

Explanation:

First, find the area and circumference of the circle using the radius and the following formulae for circles:

$Circumference = 2\pi r$

$Area = \pi r^2$

Substituting in 3 for yields:

$Circumference = 6\pi \ cm$

$Area = 9\pi \ cm^2$

Next, find what fraction of the total circumference is between the two points on the circle (the arc length).

$\frac{Arc \ Length }{Circumference } = \frac{\pi}{6\pi} = \frac{1}{6}$

Finally, use this fraction to calculate the area of the enclosed sector. Note that this area is proportional to the above fraction. In other words:

$\frac{Arc \ Length }{Circumference } = \frac{Sector \ Area}{Total \ Area}$

So the Sector Area is one sixth of the total area.

$\frac{1 }{6} = \frac{Sector \ Area}{9\pi}$

Cross multiply:

$Sector \ Area\times6 = 9\pi$

Divide both sides by 6, then simplify to get the final answer:

$Sector \ Area = \frac{9\pi}{6} = \frac{3\pi}{2}\; cm^2$

Report an Error

Example Question #2 : Arc Length And Area Of A Sector

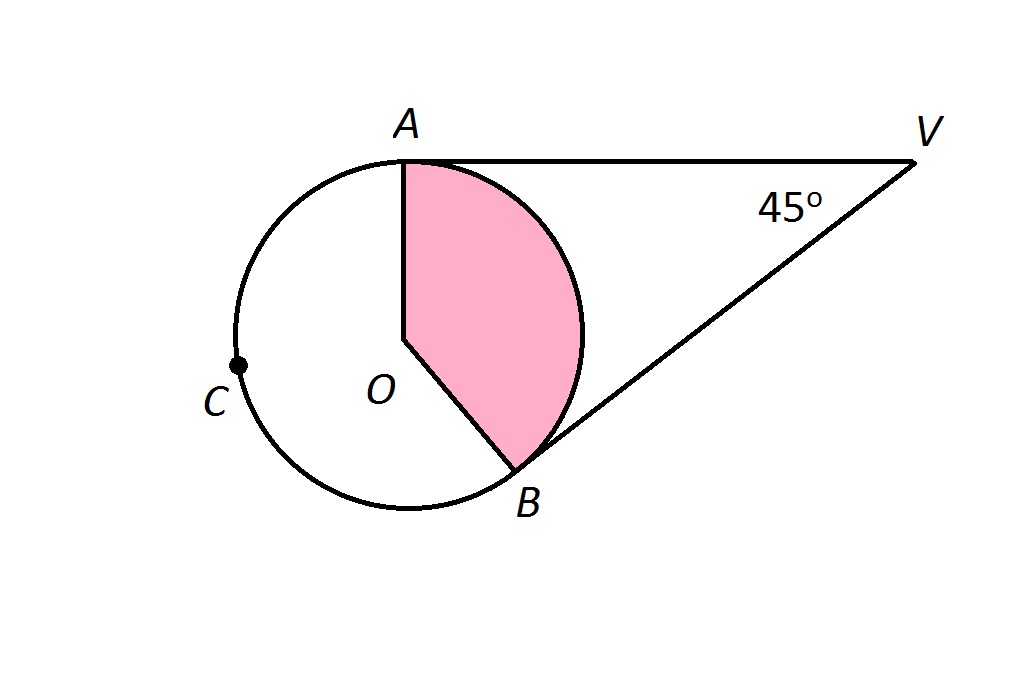
Intercepted 2

is the center of the above circle, and AO = 6 . Evaluate the length of $\overarc{AB}$ .

Possible Answers:

$\frac{9}{2} \pi$

$\frac{15}{4} \pi$

$\frac{15}{2} \pi$

$6 \pi$

$\frac{9}{4} \pi$

Correct answer:

$\frac{9}{2} \pi$

Explanation:

The radius of the circle is given to be r= AO = 6 . The total circumference of the circle is $2 \pi$ times this, or

$C = 2 \pi r = 2 \pi (6)= 12\pi$ .

The length of $\overarc{AB}$ is equal to

$l = \frac{m \overarc {AB}}{360} \cdot C$

Thus, it is first necessary to find the degree measure of $\overarc{AB}$ . If the sides of an angle with vertex outside the circle are both tangent to the circle, the angle formed is half the difference of the measures of the arcs. Therefore,

$\frac{m \overarc{ACB} - m \overarc{AB} }{2} = m \angle AVB$

Letting $x= m \overarc{AB}$ , since the total arc measure of a circle is 360 degrees,

$m \overarc{ACB} = 360 - x$

We are also given that

$m \angle AVB = 45$

Making substitutions, and solving for :

$\frac{(360- x )- x }{2} =45$

$\frac{360- 2 x }{2} =45$

Multiply both sides by 2:

$\frac{360- 2 x }{2} \cdot 2 =45 \cdot 2$

360- 2 x = 90

Subtract 360 from both sides:

360- 2 x - 360 = 90 - 360

-2x = -270

Divide both sides by :

$-2x \div (-2) = -270 \div (-2)$

x = 135 ,

the degree measure of $\overarc{AB}$ .

Thus, the length of $\overarc{AB}$ is

$l = \frac{m \overarc {AB}}{360} \cdot C$

$= \frac{225}{360} \cdot (12 \pi)$

$= \frac{3}{8} (12\pi)$

$= \frac{36}{8} \pi$

$= \frac{9}{2} \pi$

Report an Error

Example Question #3 : Arc Length And Area Of A Sector

Intercepted 2

is the center of the above circle, and AO = 8 . Evaluate the area of the shaded sector.

Possible Answers:

The information given is insufficient to answer the question.

$40 \pi$

$24 \pi$

$12 \pi$

$20 \pi$

Correct answer:

$24 \pi$

Explanation:

The radius of the circle is given to be r= AO = 8 . The total area of the circle can be found using the area formula:

$A = \pi r^{2}$

$A = \pi (8^{2})$

$A =64 \pi$

The area of the sector is equal to

$a = \frac{m \overarc {AB}}{360} \cdot A$

$\frac{m \overarc{ACB} - m \overarc{AB} }{2} = m \angle AVB$

Letting $x= m \overarc{AB}$ , since the total arc measure of a circle is 360 degrees,

$m \overarc{ACB} = 360 - x$

We are also given that

$m \angle AVB = 45$

Making substitutions, and solving for :

$\frac{(360- x )- x }{2} =45$

$\frac{360- 2 x }{2} =45$

Multiply both sides by 2:

$\frac{360- 2 x }{2} \cdot 2 =45 \cdot 2$

360- 2 x = 90

Subtract 360 from both sides:

360- 2 x - 360 = 90 - 360

-2x = -270

Divide both sides by :

$-2x \div (-2) = -270 \div (-2)$

x = 135 ,

the degree measure of $\overarc{AB}$ .

Thus, the area of the shaded sector is

$a = \frac{m \overarc {AB}}{360} \cdot A$

$= \frac{135}{360} \cdot (64 \pi)$

$= \frac{3}{8} \cdot 64 \pi$

$= \frac{192}{8} \pi$

$=24 \pi$

Report an Error

Example Question #4 : Arc Length And Area Of A Sector

Intercepted 2

is the center of the above circle, and AO = 6 . Evaluate the area of the shaded sector.

Possible Answers:

$\frac{27}{2} \pi$

$\frac{45}{2} \pi$

The information given is insufficient to answer the question.

$\frac{45}{4} \pi$

$\frac{27}{4} \pi$

Correct answer:

$\frac{45}{2} \pi$

Explanation:

The radius of the circle is given to be r= AO = 6 . The total area of the circle can be found using the area formula:

$A = \pi r^{2}$

$A = \pi (6^{2})$

$A =36\pi$

The area of the sector is equal to

$a = \frac{m \overarc {ACB}}{360} \cdot A$

Thus, it is first necessary to find the degree measure of $\overarc{ACB}$ . If the sides of an angle with vertex outside the circle are both tangent to the circle, the angle formed is half the difference of the measures of the arcs. Therefore,

$\frac{m \overarc{ACB} - m \overarc{AB} }{2} = m \angle AVB$

Letting $x= m \overarc{ACB}$ , since the total arc measure of a circle is 360 degrees,

$m \overarc{AB} = 360 - x$

We are also given that

$m \angle AVB = 45$

Making substitutions, and solving for :

$\frac{x- (360- x ) }{2} =45$

$\frac{ 2 x -360 }{2} =45$

Multiply both sides by 2:

$\frac{2 x -360}{2} \cdot 2 =45 \cdot 2$

2 x -360 = 90

Add 360 to both sides:

2 x -360+ 360 = 90 + 360

2 x= 450

Divide both sides by 2:

$2 x \div 2 = 450 \div 2$

x = 225 ,

the degree measure of $\overarc{ACB}$ .

Therefore, the area of the shaded sector is

$a = \frac{m \overarc {ACB}}{360} \cdot A$

$= \frac{225}{360} \cdot 36 \pi$

$= \frac{5}{8 } \cdot 36 \pi$

$= \frac{180}{8 } \pi$

$= \frac{45}{2} \pi$

Report an Error

Example Question #21 : Properties Of Polygons And Circles

Intercepted 2

is the center of the above circle, and AO = 8 . Evaluate the length of $\overarc{ACB}$ .

Possible Answers:

$3 \pi$

$6 \pi$

$10 \pi$

$5 \pi$

$12 \pi$

Correct answer:

$10 \pi$

Explanation:

The radius of the circle is given to be r= AO = 8 .

The total circumference of the circle is $2 \pi$ times this, or

$C = 2 \pi r = 2 \pi (8)= 16\pi$ .

The length of $\overarc{ACB}$ is equal to

$l= \frac{m \overarc {ACB}}{360} \cdot C$

$\frac{m \overarc{ACB} - m \overarc{AB} }{2} = m \angle AVB$

Letting $x= m \overarc{ACB}$ , since the total arc measure of a circle is 360 degrees,

$m \overarc{AB} = 360 - x$

We are also given that

$m \angle AVB = 45$

Making substitutions, and solving for :

$\frac{x- (360- x ) }{2} =45$

$\frac{ 2 x -360 }{2} =45$

Multiply both sides by 2:

$\frac{2 x -360}{2} \cdot 2 =45 \cdot 2$

2 x -360 = 90

Add 360 to both sides:

2 x -360+ 360 = 90 + 360

2 x= 450

Divide both sides by 2:

$2 x \div 2 = 450 \div 2$

x = 225 ,

the degree measure of $\overarc{ACB}$ .

Thus, the length of $\overarc{ACB}$ is

$l = \frac{m \overarc {ACB}}{360} \cdot C$

$= \frac{225}{360} \cdot 16 \pi$

$= \frac{5}{8} \cdot 16 \pi$

$= \frac{80}{8} \pi$

$= 10 \pi$

Report an Error

Example Question #1 : Arc Length And Area Of A Sector

Intercepted

Refer to the above figure. Give the ratio of the area of Sector 2 to that of Sector 1.

Possible Answers:

16:1

4:1

25:1

6:1

5:1

Correct answer:

5:1

Explanation:

The ratio of the area of the larger Sector 2 to that of smaller Sector 1 is equal to the ratio of their respective arc measures - that is,

$m \overarc{ACB} : m \overarc{AD}$ .

Therefore, it is sufficient to find these arc measures.

If the sides of an angle with vertex outside the circle are both tangent to the circle, the angle formed is half the difference of the measures of the arcs. Therefore,

$\frac{m \overarc{ACB} - m \overarc{AB} }{2} = m \angle AVB$

Letting $x= m \overarc{ACB}$ , since the total arc measure of a circle is 360 degrees,

$m \overarc{AB} = 360 - x$

We are also given that

$m \angle AVB = 45$

Making substitutions, and solving for :

$\frac{x- (360- x ) }{2} =45$

$\frac{ 2 x -360 }{2} =45$

Multiply both sides by 2:

$\frac{2 x -360}{2} \cdot 2 =45 \cdot 2$

2 x -360 = 90

Add 360 to both sides:

2 x -360+ 360 = 90 + 360

2 x= 450

Divide both sides by 2:

$2 x \div 2 = 450 \div 2$

x = 225 ,

the degree measure of $\overarc{ACB}$ .

It follows that

$m \overarc{AB} = 360 - 225 = 135$

By the Arc Addition Principle,

$m \overarc{AB} = m \overarc{AD} + m \overarc{DB}$

Since $\angle DOB$ , the central angle which intercepts $\overarc{DB}$ , is a right angle, $m \overarc{DB} = 90$ . By substitution,

$135 = m \overarc{AD} + 90$ ,

and

$135 - 90 = m \overarc{AD} + 90 - 90$

$45= m \overarc{AD}$

The ratio $m \overarc{ACB} : m \overarc{AD}$ is equal to

$\frac{225}{45} = \frac{225 \div 45}{45 \div 45 } = \frac{5}{1}$ ,

a 5 to 1 ratio.

Report an Error

View Tutors

Garth
Certified Tutor

View Tutors

Kinza
Certified Tutor

University of Georgia, Bachelor of Science, Biology, General.

View Tutors

Rosanna
Certified Tutor

Universidad Autónoma de Santo Domingo, Bachelor in Arts, Psychology. Universidad Autonoma de Santo Domingo, Master of Arts, M...

All HiSET: Math Resources

125 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Algebra Tutors in San Diego, Algebra Tutors in Chicago, GRE Tutors in San Francisco-Bay Area, Spanish Tutors in Washington DC, Computer Science Tutors in New York City, MCAT Tutors in San Francisco-Bay Area, SAT Tutors in San Diego, GMAT Tutors in Phoenix, SAT Tutors in Miami, GMAT Tutors in Washington DC

Popular Courses & Classes

SAT Courses & Classes in Los Angeles, MCAT Courses & Classes in Chicago, Spanish Courses & Classes in Philadelphia, GRE Courses & Classes in Houston, GMAT Courses & Classes in New York City, LSAT Courses & Classes in Atlanta, GMAT Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in San Diego

Popular Test Prep

LSAT Test Prep in Denver, SAT Test Prep in Seattle, LSAT Test Prep in Atlanta, ISEE Test Prep in New York City, ACT Test Prep in Boston, ACT Test Prep in Miami, SAT Test Prep in Miami, ACT Test Prep in San Diego, LSAT Test Prep in San Francisco-Bay Area, GRE Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

HiSET: Math : HiSet: High School Equivalency Test: Math

Study concepts, example questions & explanations for HiSET: Math

All HiSET: Math Resources

Example Questions

Example Question #1 : Perimeter And Circumference

Example Question #81 : Hi Set: High School Equivalency Test: Math

Example Question #82 : Hi Set: High School Equivalency Test: Math

Example Question #1 : Perimeter And Circumference

Example Question #1 : Arc Length And Area Of A Sector

Example Question #2 : Arc Length And Area Of A Sector

Example Question #3 : Arc Length And Area Of A Sector

Example Question #4 : Arc Length And Area Of A Sector

Example Question #21 : Properties Of Polygons And Circles

Example Question #1 : Arc Length And Area Of A Sector

All HiSET: Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: