Call Now to Set Up Tutoring:

(888) 888-0446

HiSET: Math : HiSet: High School Equivalency Test: Math

Study concepts, example questions & explanations for HiSET: Math

Create An Account

All HiSET: Math Resources

125 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : Angle Measure, Central Angles, And Inscribed Angles

Inscribed heptagon

The above figure shows a regular seven-sided polygon, or heptagon, inscribed inside a circle. is the common center of the figures.

Give the measure of $\angle DBO$ .

Possible Answers:

$63\frac{3}{7}^{\circ }$

$65 \frac{1}{7}^{\circ }$

$62 \frac{4}{7}^{\circ }$

$64 \frac{2}{7}^{\circ }$

$61 \frac{5}{7}^{\circ }$

Correct answer:

$64 \frac{2}{7}^{\circ }$

Explanation:

Consider the figure below, which adds some radii of the heptagon (and circle):

Inscribed heptagon

$\overline{OB}$ , as a radius of a regular polygon, bisects $\angle EBD$ . The measure of this angle can be calculated using the formula

$m = \frac{180 (n-2)}{n}$ ,

where n = 7 :

$m \angle EBD = \frac{180^{\circ } (7-2)}{7} = \frac{180^{\circ } (5)}{7} = \frac{900}{7}^{\circ } = 1 28 \frac{4}{7}^{\circ }$

Consequently,

$\angle DBO = \frac{1}{2} \cdot m \angle EBD = \frac{1}{2} \cdot 1 28 \frac{4}{7}^{\circ } = 64 \frac{2}{7}^{\circ }$ ,

the correct response.

Report an Error

Example Question #1 : Properties Of Polygons And Circles

Inscribed heptagon

The above figure shows a regular seven-sided polygon, or heptagon, inscribed inside a circle. is the common center of the figures.

Give the measure of $\angle AOB$ .

Possible Answers:

$156 \frac{4}{7}^{\circ }$

$155 \frac{1}{7}^{\circ }$

$154 \frac{2}{7}^{\circ }$

$152 \frac{6}{7}^{\circ }$

$153 \frac{5}{7}^{\circ }$

Correct answer:

$154 \frac{2}{7}^{\circ }$

Explanation:

Examine the diagram below, which divides $\angle AOB$ into three congruent angles, one of which is $\angle 1$ :

Inscribed heptagon

The measure of a central angle of a regular -sided polygon which intercepts one side of the polygon is $\frac{360 ^{\circ }}{n}$ ; setting n = 7 , the measure of $\angle 1$ is

$m \angle 1 = \frac{360 ^{\circ }}{7} = 51 \frac{3}{7}^{\circ }$ . $\angle AOC$ has measure three times this; that is,

$m \angle AOC = 3 \times51 \frac{3}{7}^{\circ } = 154 \frac{2}{7}^{\circ }$

Report an Error

Example Question #11 : Measurement And Geometry

Inscribed heptagon

The above figure shows a regular seven-sided polygon, or heptagon, inscribed inside a circle. is the common center of the figures.

Give the measure of $\angle AOC$ .

Possible Answers:

$105 \frac{1}{7}^{\circ }$

$101 \frac{3}{7}^{\circ }$

$103 \frac{5}{7}^{\circ }$

$102 \frac{6}{7}^{\circ }$

$104 \frac{2}{7}^{\circ }$

Correct answer:

$102 \frac{6}{7}^{\circ }$

Explanation:

Examine the diagram below, which divides $\angle AOC$ into two congruent angles, one of which is $\angle 1$ :

Inscribed heptagon

The measure of a central angle of a regular -sided polygon which intercepts one side of the polygon is $\frac{360 ^{\circ }}{n}$ ; setting n = 7 , the measure of $\angle 1$ is

$m \angle 1 = \frac{360 ^{\circ }}{7} = 51 \frac{3}{7}^{\circ }$ . $\angle AOC$ has measure twice this; that is,

$m \angle AOC = 2 \times51 \frac{3}{7}^{\circ } = 102 \frac{6}{7}^{\circ }$

Report an Error

Example Question #6 : Angle Measure, Central Angles, And Inscribed Angles

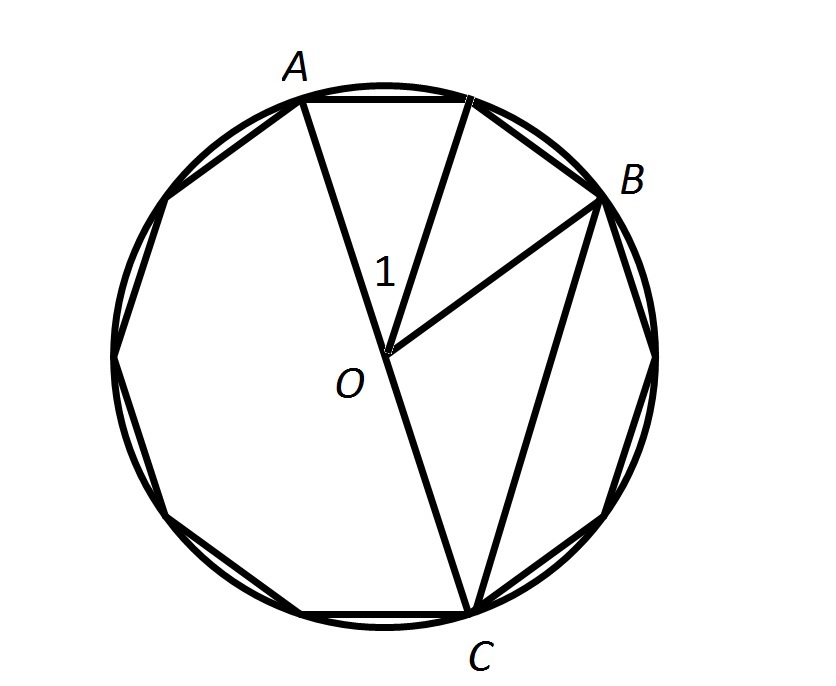
Inscribed nonagon

The above figure shows a regular ten-sided polygon, or decagon, inscribed inside a circle. is the common center of the figures.

Give the measure of $\angle AOB$ .

Possible Answers:

$75^{\circ }$

$72^{\circ }$

$80^{\circ }$

$84^{\circ }$

$76^{\circ }$

Correct answer:

$72^{\circ }$

Explanation:

Examine the diagram below, which divides $\angle AOB$ into two congruent angles, one of which is $\angle 1$ :

Inscribed nonagon

The measure of a central angle of a regular -sided polygon which intercepts one side of the polygon is $\frac{360 ^{\circ }}{n}$ ; setting n = 10 , the measure of $\angle 1$ is

$m \angle 1 = \frac{360 ^{\circ }}{10} =36^{\circ }$ . $\angle AOB$ has measure twice this; that is,

$m \angle AOB = 2 \times 36 ^{\circ } = 72 ^{\circ }$ .

Report an Error

Example Question #7 : Angle Measure, Central Angles, And Inscribed Angles

Inscribed nonagon

The above figure shows a regular ten-sided polygon, or decagon, inscribed inside a circle. is the common center of the figures.

Give the measure of $\angle OBC$ .

Possible Answers:

$32^{\circ }$

$42^{\circ }$

$45^{\circ }$

$40^{\circ }$

$36 ^{\circ }$

Correct answer:

$36 ^{\circ }$

Explanation:

Consider the triangle $\bigtriangleup OBC$ . Since $\overline{OB}$ and $\overline{OC}$ are radii, they are congruent, and by the Isosceles Triangle Theorem, $m \angle OBC = m \angle OCB$ .

Now, examine the figure below, which divides $\angle BOC$ into three congruent angles, one of which is $\angle 1$ :

Inscribed nonagon

The measure of a central angle of a regular -sided polygon which intercepts one side of the polygon is $\frac{360 ^{\circ }}{n}$ ; setting n = 10 , the measure of $\angle 1$ is

$m \angle 1 = \frac{360 ^{\circ }}{10} =36^{\circ }$ . $\angle BOC$ has measure three times this; that is,

$m \angle BOC = 3 \times 36 ^{\circ } = 108 ^{\circ }$ .

The measures of the interior angles of a triangle total $108^{\circ }$ , so

$m \angle OCB + m \angle OBC+m \angle BOC = 180$

Substituting 108 for $\angle BOC$ and $m \angle OBC$ for $m \angle OCB$ :

$m \angle OBC+ m \angle OBC+108 = 180$

$2 m \angle OBC+108 = 180$

$2 m \angle OBC+108- 108 = 180- 108$

$2 m \angle OBC=72$

$2 m \angle OBC \div 2 =72 \div 2$

$m \angle OBC= 36$

Report an Error

Example Question #1 : Angle Measure, Central Angles, And Inscribed Angles

Inscribed nonagon

The above figure shows a regular ten-sided polygon, or decagon, inscribed inside a circle. is the common center of the figures.

Give the measure of $\angle CBE$ .

Possible Answers:

$30^{\circ }$

$32^{\circ }$

$42^{\circ }$

$36^{\circ }$

$40^{\circ }$

Correct answer:

$36^{\circ }$

Explanation:

Through symmetry, it can be seen that Quadrilateral BCDE is a trapezoid, such that $\overline{BC} || \overline{DE }$ . By the Same-Side Interior Angle Theorem, $\angle CBE$ and $\angle DEB$ are supplementary - that is,

$m \angle CBE +\angle DEB = 180$ .

The measure of $\angle DEB$ can be calculated using the formula

$m = \frac{180 (n-2)}{n}$ ,

where n = 10 :

$m \angle DEB= \frac{180^{\circ } (10-2)}{10} = \frac{180^{\circ } (8)}{10} = \frac{1,440}{10}^{\circ } =144 ^{\circ }$

Substituting:

$m \angle CBE +144= 180$

$m \angle CBE +144 - 144 = 180 - 144$

$m \angle CBE = 36$

Report an Error

Example Question #1 : Properties Of Polygons And Circles

If two angles are supplementary and one angle measures $95^{\circ}$ , what is the measurement of the second angle?

Possible Answers:

$80^{\circ}$

$90^{\circ}$

$95^{\circ}$

$85^{\circ}$

Correct answer:

$85^{\circ}$

Explanation:

Step 1: Define supplementary angles. Supplementary angles are two angles whose sum is $180^{\circ}$ .

Step 2: Find the other angle by subtracting the given angle from the maximum sum of the two angles.

So, $180^{\circ}-95^{\circ}=85^\circ$

The missing angle (or second angle) is $85^{\circ}$

Report an Error

Example Question #2 : Properties Of Polygons And Circles

$\angle 1$ and $\angle 2$ are complementary angles.

$\angle 1$ and $\angle 3$ are supplementary angles.

$\angle 2 \cong \angle 4$

$m \angle 3= 112^{\circ }$

Evaluate $m \angle 4$ .

Possible Answers:

$112^{\circ }$

$90^{\circ }$

$158^{\circ }$

$68^{\circ }$

$22^{\circ }$

Correct answer:

$22^{\circ }$

Explanation:

$\angle 1$ and $\angle 3$ are supplementary angles, so, by definition,

$m \angle 1 + m \angle 3 = 180^{\circ }$

$m \angle 3= 112^{\circ }$ , so substitute and solve for $m \angle 1$ :

$m \angle 1 + 112^{\circ } = 180^{\circ }$

$m \angle 1 + 112^{\circ } -112^{\circ } = 180^{\circ }-112^{\circ }$

$m \angle 1 = 68 ^{\circ }$

$\angle 1$ and $\angle 2$ are complementary angles, so, by definition,

$m \angle 1 + m \angle 2 = 90^{\circ }$

Substitute and solve for $m \angle 2$ :

$68 ^{\circ } + m \angle 2 = 90^{\circ }$

$68 ^{\circ } + m \angle 2 - 68 ^{\circ } = 90^{\circ }-68 ^{\circ }$

$m \angle 2 =22^{\circ }$

$\angle 2 \cong \angle 4$ - that is, the angles have the same measure. Therefore,

$m \angle 4 =22^{\circ }$ .

Report an Error

Example Question #71 : Hi Set: High School Equivalency Test: Math

$\angle 1$ and $\angle 2$ are a pair of vertical angles.

$\angle 3$ and $\angle 4$ are a linear pair.

$\angle 2$ and $\angle 3$ are the two acute angles of a right triangle.

Which of the following must be true?

Possible Answers:

$m \angle 1 = m \angle 4$

$m \angle 4 + 90^{\circ }= m \angle 1$

$m \angle 1 + 90^{\circ }= m \angle 4$

$m \angle 1 +m \angle 4 = 180^{\circ }$

$m \angle 1 +m \angle 4 = 90^{\circ }$

Correct answer:

$m \angle 1 + 90^{\circ }= m \angle 4$

Explanation:

$\angle 1$ and $\angle 2$ are a pair of vertical angles; it follows that

$m \angle 1 = m \angle 2$

$\angle 3$ and $\angle 4$ are a linear pair; it follows that they are supplementary - that is,

$m \angle 3 + m \angle 4 = 180^{\circ }$ .

$\angle 2$ and $\angle 3$ are the two acute angles of a right triangle; it follows that they are complementary - that is,

$m \angle 2 + m \angle 3 = 90^{\circ }$ .

Therefore, we have the three statements

$m \angle 1 = m \angle 2$

$m \angle 2 + m \angle 3 = 90^{\circ }$

$m \angle 3 + m \angle 4 = 180^{\circ }$

From the second statement, we can subtract $m \angle 2$ from both sides to get

$m \angle 2 + m \angle 3 - m \angle 2 = 90^{\circ } - m \angle 2$

$m \angle 3 = 90^{\circ } - m \angle 2$

Substitute this expression for $m \angle 3$ in the third expression to get

$90^{\circ } - m \angle 2 + m \angle 4 = 180^{\circ }$

Substitute $m \angle 1$ for $m \angle 2$ :

$90^{\circ } - m \angle 1 + m \angle 4 = 180^{\circ }$

Add $m \angle 1 - 90^{\circ }$ to both sides:

$90^{\circ } - m \angle 1 + m \angle 4 +m \angle 1 - 90^{\circ }= 180^{\circ }+m \angle 1 - 90^{\circ }$

$m \angle 4 = 90^{\circ }+m \angle 1$ ,

or, rearranged,

$m \angle 1 + 90^{\circ }= m \angle 4$ .

Report an Error

Example Question #72 : Hi Set: High School Equivalency Test: Math

A five sided irregular polygon has sides of the following lengths:

$1,\ 4,\ 7,\ 8,\ \textup{and } 13$

Find its perimeter.

Possible Answers:

Correct answer:

Explanation:

Perimeters can be calculated using the following formula.

P=s_1+s_2+s_3...

In this formula, the variable, , represents a side of the polygon.

Substitute and solve.

P=1+4+7+8+13

P=33

Report an Error

View Tutors

Megha
Certified Tutor

North Carolina State University at Raleigh, Bachelor of Science, Biology, General. St. George's University, Doctor of Medicin...

View Tutors

Priyanvada
Certified Tutor

University of North Texas, Doctor of Philosophy, Materials Engineering.

View Tutors

Lucinda
Certified Tutor

South University-Savannah, Bachelor of Science, Health Services Administration.

All HiSET: Math Resources

125 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GRE Tutors in Philadelphia, Calculus Tutors in Denver, LSAT Tutors in Denver, Chemistry Tutors in Miami, Math Tutors in Seattle, Physics Tutors in Los Angeles, Math Tutors in San Francisco-Bay Area, Chemistry Tutors in Philadelphia, LSAT Tutors in San Diego, Calculus Tutors in Los Angeles

Popular Courses & Classes

SSAT Courses & Classes in Seattle, SAT Courses & Classes in Seattle, SSAT Courses & Classes in Philadelphia, GMAT Courses & Classes in Houston, MCAT Courses & Classes in Los Angeles, Spanish Courses & Classes in San Diego, Spanish Courses & Classes in Atlanta, MCAT Courses & Classes in Houston, MCAT Courses & Classes in Miami, ACT Courses & Classes in Dallas Fort Worth

Popular Test Prep

GMAT Test Prep in New York City, GRE Test Prep in Boston, ACT Test Prep in San Diego, MCAT Test Prep in Dallas Fort Worth, MCAT Test Prep in Seattle, GRE Test Prep in New York City, MCAT Test Prep in Los Angeles, LSAT Test Prep in Phoenix, GMAT Test Prep in Houston, MCAT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

HiSET: Math : HiSet: High School Equivalency Test: Math

Study concepts, example questions & explanations for HiSET: Math

All HiSET: Math Resources

Example Questions

Example Question #2 : Angle Measure, Central Angles, And Inscribed Angles

Example Question #1 : Properties Of Polygons And Circles

Example Question #11 : Measurement And Geometry

Example Question #6 : Angle Measure, Central Angles, And Inscribed Angles

Example Question #7 : Angle Measure, Central Angles, And Inscribed Angles

Example Question #1 : Angle Measure, Central Angles, And Inscribed Angles

Example Question #1 : Properties Of Polygons And Circles

Example Question #2 : Properties Of Polygons And Circles

Example Question #71 : Hi Set: High School Equivalency Test: Math

Example Question #72 : Hi Set: High School Equivalency Test: Math

All HiSET: Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: