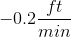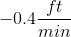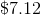All HiSET: Math Resources
Example Questions
Example Question #4 : Estimate Rate Of Change From A Graph

Above is the graph of a function




The average rate of change of a function 


Restated, it is the slope of the line that passes through 

To find the correct value of 



The 
Example Question #281 : Hi Set: High School Equivalency Test: Math
Consider the following statement:
"If an integer is odd and is between 10 and 20, then it must be prime."
Which of the following is a counterexample to the statement?
The integer 16 is not prime.
The integer 15 is not prime.
The integer 9 is not prime.
Odd numbers are not evenly divisible by 2.
The integer 13 is prime.
The integer 15 is not prime.
A counterexample is a single example that disproves a statement. In order to disprove "If an integer is odd and is between 10 and 20, then it must be prime," you must show that there is an integer that is odd and is between 10 and 20, but is not prime.
While 9 is odd and is not prime, it is not between 10 and 20. 16 is also not prime, but it is not odd.
15 is the answer because it is odd and is between 10 and 20, but is not prime, because it is divisible by 5 and 3, in addition to being divisible by itself and 1.
Example Question #1 : Make Inferences Or Predictions Based On Data Or Information
A swimming pool was drained of water. At 8:56 AM, the water in the pool was 5.7 ft high. At 9:10 AM, the water level in the pool was 2.9 ft high.
Using this information, determine the average rate of change in water height during this period of time.
The value we are trying to find is an average rate of decrease. In other words, we are looking for how much, on average, the water level decreased in a minute. To find the average, take the total difference in water level and divide it by the total difference in time.
The total change in water height is given by the ending height minus the starting height:
The total change in time is the amount of minutes that pass between 8:56 AM and 9:10 PM:
Therefore, the average rate of decrease is 
Example Question #131 : Measurement And Geometry
Two of a triangle's interior angles measure 


A triangle that has interior angles of 



Since we know this triangle is a 30-60-90 triangle, we can use the special ratios that always hold true for this triangle's sides and angles to figure out the lengths of its other sides. The following ratio holds true for all 30-60-90 triangles, where the side in a fraction with a given angle is the side opposite that angle.
We're told that the hypotenuse of our triangle has a length of 




As you can see, for this particular triangle, 








Thus, the correct answer is 
Example Question #4 : Understand Right Triangles
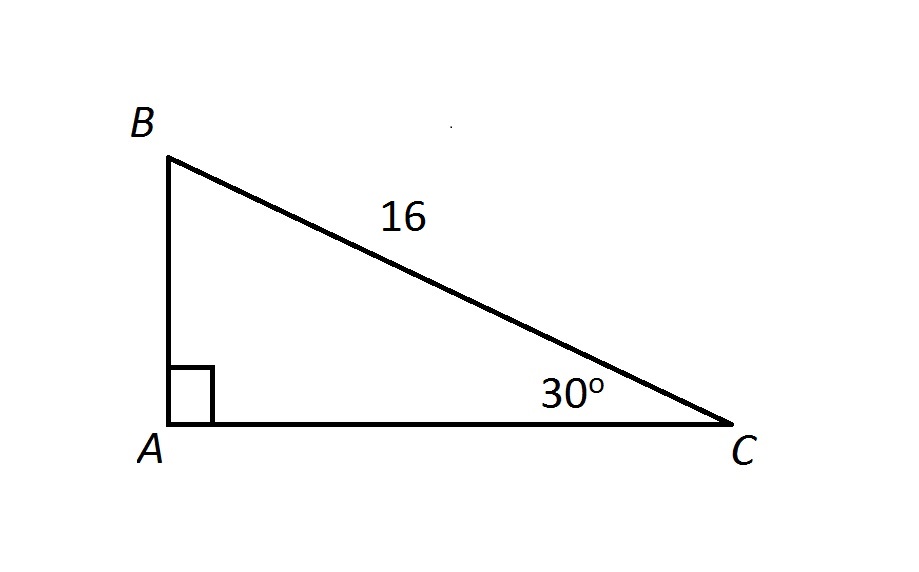
Examine the above triangle. Which of the following correctly gives the area of 
None of the other choices gives the correct response.
Since 



making 
By the 30-60-90 Triangle Theorem,

and
Refer to the diagram below:
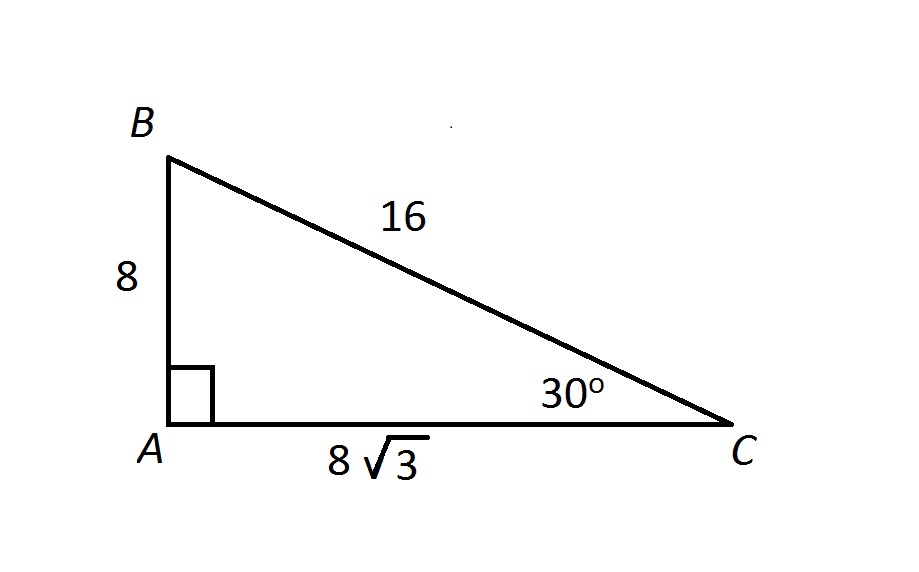
The area of a right triangle is equal to half the product of the lengths of its legs, so

the correct response.
Example Question #5 : Understand Right Triangles
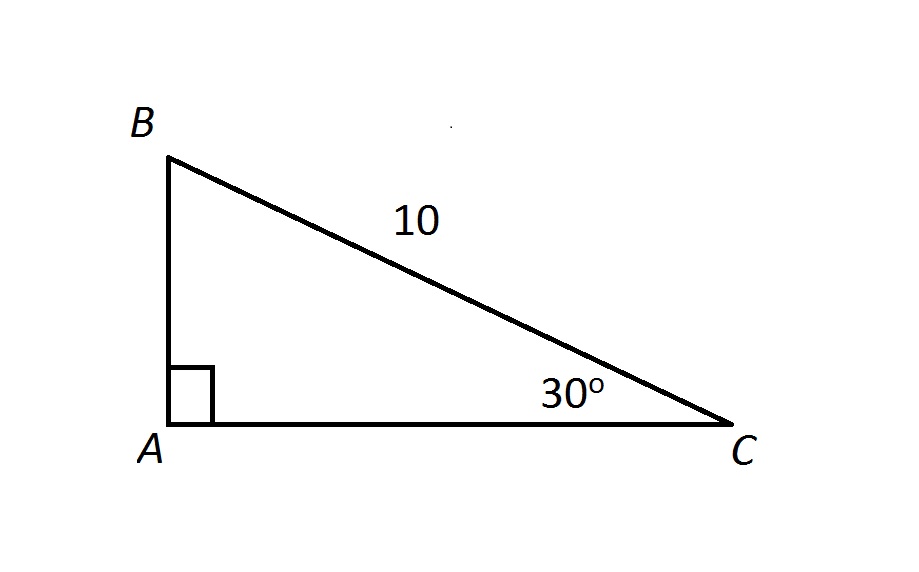
Examine the above triangle. Which of the following correctly gives the perimeter of 
Since 



making 
By the 30-60-90 Triangle Theorem,

and
Refer to the diagram below:
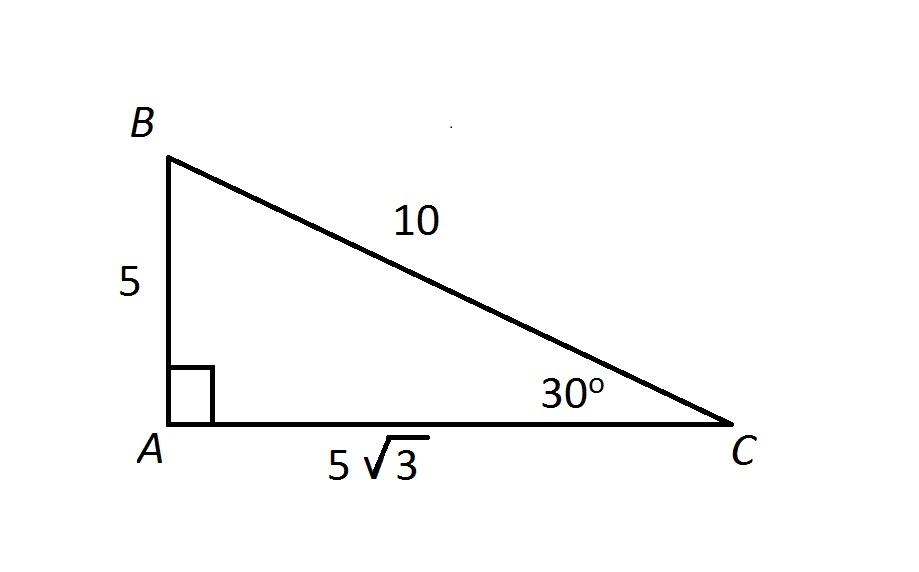
The perimeter - the sum of the sidelengths - is

Example Question #1 : Mathematical Process Categories
Three friends go in on a pizza, which costs $10.49 before 6% tax. Mike agrees to pay $4, and Mickey and Morris agree to split the remainder of the cost evenly. How much will Morris pay?
6% of 10.49 is equal to

which, to the nearest cent, rounds to 
Add this tax to the price of the pizza; the amount paid is
Mike pays $4, so Morris will pay half the remainder, or

Example Question #2 : Mathematical Process Categories
Which of the following would be a reasonable answer to the question
"What is the length of a candy bar?"
Ten kilograms
Ten kilowatts
Ten centimeters
Ten milliliters
Ten hectares
Ten centimeters
The question is asking for unit of length. Of the units given in the five choices, only centimeters is a unit of length, and ten centimeters—the metric equivalent of about four inches—is a reasonable length for a candy bar.
Of the other units:
The kilogram is a unit of mass which corresponds to a little over two ounces.
The hectare is a unit of area, usually land, and is equivalent to about two and a half acres.
The milliliter is a very small unit of volume.
The kilowatt is a unit of power.
All HiSET: Math Resources