All HiSET: Math Resources
Example Questions
Example Question #1 : Prove Relationships In Geometric Figures
Given: 


Does sufficient information exist to prove that 


Insufficient information exists to prove that 


Insufficient information exists to prove that 
We are given that, between the triangles, two pairs of corresponding sides are proportional. Without knowing anything else, the proportionality of two pairs of sides is insufficient to prove that the triangles are similar.
Example Question #1 : Measurement And Geometry
Given: 



Does sufficient information exist to prove that 

Insufficient information exists to prove that 




We are given that, between the triangles, two pairs of corresponding sides are proportional, and that a pair of corresponding angles are congruent. The angles that are congruent are the included angles of their respective sides. By the SAS Similarity Postulate, this is enough to prove that 
Example Question #1 : Prove Relationships In Geometric Figures


Complete the sentence: the area of 

(Select the closest whole percent)
The ratio of the areas of two similar triangles is equal to the square of their scale factor. The scale factor is equal to 

This makes the area of larger triangle 



Example Question #1 : Measurement And Geometry
Given: 



Does sufficient information exist to prove that 


Insufficient information exists to prove that 


Insufficient information exists to prove that 
We are given that, between the triangles, two pairs of corresponding sides are proportional, and that a pair of corresponding angles are congruent. If the angles were the included angles of the triangles, then the SAS Similarity Theorem could be applied to prove that 
Example Question #2 : Measurement And Geometry


Complete the sentence: the area of 

(Select the closest whole percent).
The ratio of the areas of two similar triangles is equal to the square of their scale factor. The scale factor is equal to 

This makes the area of smaller triangle 



Example Question #3 : Prove Relationships In Geometric Figures


Complete the sentence: the perimeter of 

(Select the closest whole percent).
The ratio of the perimeters of two similar triangles is equal to their scale factor. This is factor is 
This makes the perimeter of larger triangle 


Example Question #4 : Prove Relationships In Geometric Figures


Complete the sentence: the perimeter of 

(Select the closest whole percent)
The ratio of the perimeters of two similar triangles is equal to their scale factor. This is factor is 
This makes the perimeter of the smaller triangle 



Example Question #10 : Congruence And Similarity Criteria For Triangles
A triangle has sides of length 8 and 12; the triangle is scalene and obtuse. Which of the following could be the length of its third side?
A scalene triangle has three sides of different lengths. The triangle is known to have sides of length 8 and 12, so this eliminates 8 and 12 as the correct choices for the length of the third side.
The sum of the lengths of the two smallest sides must exceed the length of the third side. 4 can be eliminated as a the correct choice, since 
This leaves 6 and 10 as possible answers. For a triangle to be obtuse, it must hold that if 


If the length of the third side is 10, setting 

violating this condition.
If the length of the third side is 6, setting 

satisfying this condition.
This makes 6 the correct choice.
Example Question #1 : Properties Of Polygons And Circles
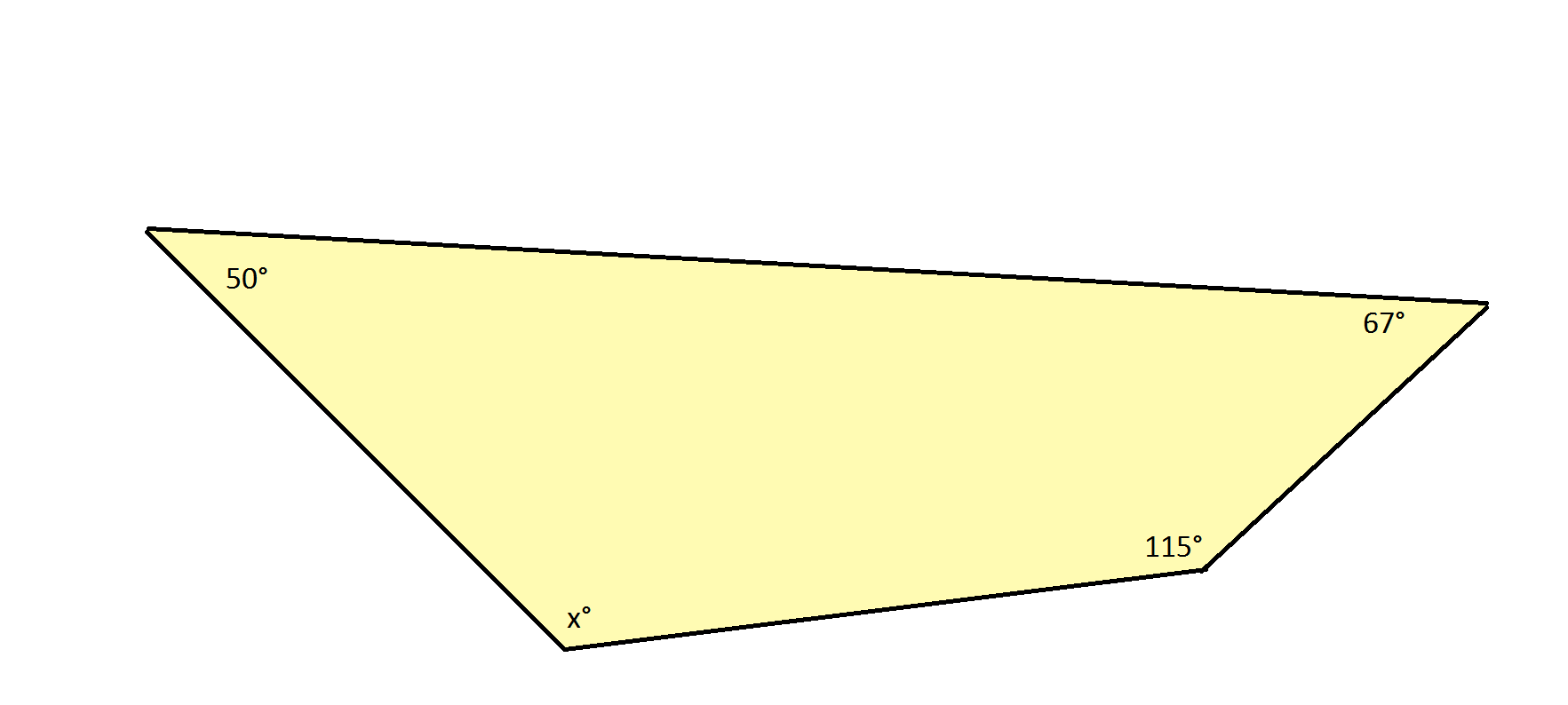
A quadrilateral is shown, and the angle measures of 3 interior angles are given. Find x, the missing angle measure.
The sum of the measures of the interior angles of a quadrilateral is 360 degrees. The sum of the measures of the interior angles of any polygon can be determined using the following formula:


For example, with a quadrilateral, which has 4 sides, you obtain the following calculation:
Solving for 
Solving for 
Example Question #11 : Measurement And Geometry
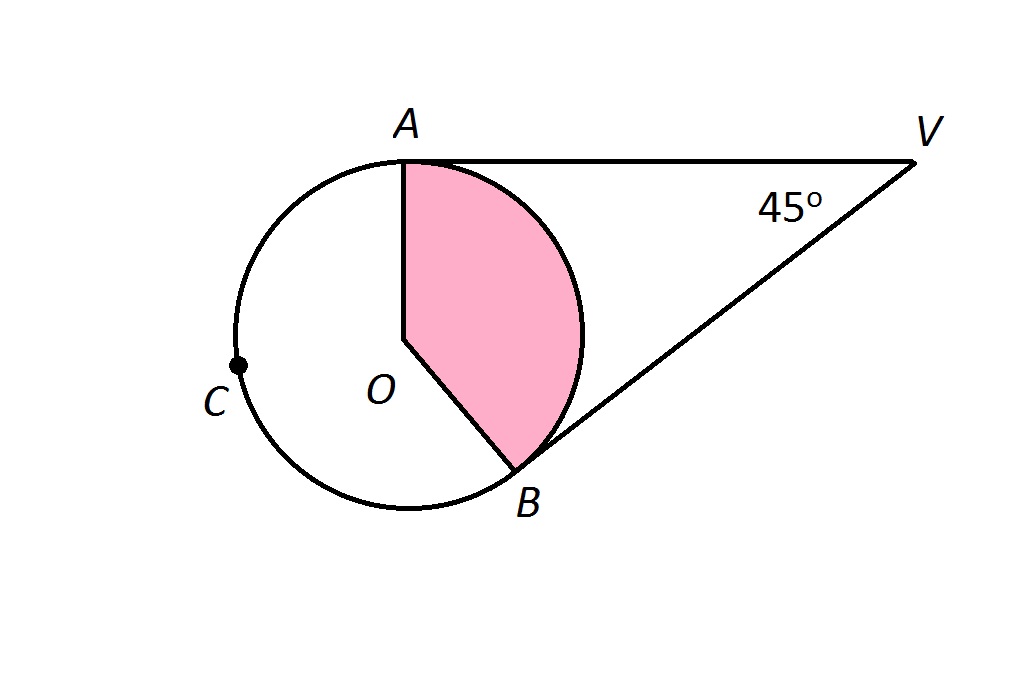





Therefore, we need to find 
If the sides of an angle with vertex outside the circle are both tangent to the circle, the angle formed is half the difference of the measures of the arcs. Therefore,
Letting 
We are also given that
Making substitutions, and solving for 
Multiply both sides by 2:
Subtract 360 from both sides:
Divide both sides by 

the measure of 

All HiSET: Math Resources





















































