All HiSET: Math Resources
Example Questions
Example Question #271 : Hi Set: High School Equivalency Test: Math
The equation
has two distinct solutions. What is their sum?
It is not necessary to actually find the solutions to a quadratic equation to determine the sum of its solutions.
First, get the equation in standard form 

If a quadratic equation has two distinct solutions, which we are given here, their sum is the linear coefficient 


Example Question #44 : Algebraic Concepts
The graph of the polynomial function
has one and only one zero on the interval 
The Intermediate Value Theorem (IVT) states that if the graph of a function 
![[a, b]](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1094264/gif.latex)












Example Question #1 : Use The Zeros To Construct A Rough Graph Of A Function
The graph of a function is shown below, with labels on the y-axis hidden.

Determine which of the following functions best fits the graph above.
Use the zeroes of the graph to determine the matching function. Zeroes are values of x where 
Visually, you can see that the curve crosses the x-axis when 


A function with a factor of 






The answer choice 



Example Question #2 : Use The Zeros To Construct A Rough Graph Of A Function

Which of the functions below best matches the graphed function?
First, look at the zeroes of the graph. Zeroes are where the function touches the x-axis (i.e. values of 

The graph shows the function touching the x-axis when 

Notice all of the possible answers are already factored. Therefore, look for one with a factor of 







This function fills the criteria; it has an 




Example Question #1 : Rate Of Change Of A Function
What is the slope of the line given by the following table?
Given two points

the formula for a slope is

Thus, since our given table is
we select two points, say

and use the slope formula to compute the slop.
Thus,

Hence, the slope of the line generated by the table is

Example Question #2 : Calculate And Interpret Rate Of Change Over A Specified Interval
Define 
Give the average rate of change of 
![[2,3]](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1094678/gif.latex)
The average rate of change of a function 
![[a, b]](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1094680/gif.latex)
Setting 
Evaluate 


the correct response.
Example Question #3 : Calculate And Interpret Rate Of Change Over A Specified Interval
Define 
Give the average rate of change of 
![[-1, 1]](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1094859/gif.latex)
The average rate of change of a function 
![[a, b]](https://cdn-s3.varsitytutors.com/uploads/formula_image/image/1094680/gif.latex)
Setting 
Evaluate 


Evaluate 


The average rate of change is therefore

Example Question #51 : Algebraic Concepts

The graph of a function is given above, with the coordinates of two points on the curve shown. Use the coordinates given to approximate the rate of change of the function between the two points.
The rate of change between two points on a curve can be approximated by calculating the change between two points.
Let 

Notice that the numerator is the overall change in y, and the denominator is the overall change in x.
The calculation for the problem proceeds as follows:
Let 

Subtract to get the final answer:
Note that it does not matter which you assign to be the first point and which you assign to be the second, as it will lead to the same value due to negatives canceling out.
Example Question #2 : Estimate Rate Of Change From A Graph

Above is the graph of a function 

The rate of change of a function 
![[a, b]](https://cdn-s3.varsitytutors.com/uploads/formula_image/image/1085449/gif.latex)

Set 

The graph passes through 



the correct response.
Example Question #3 : Estimate Rate Of Change From A Graph

Above is the graph of a function 


![[1, 5]](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1085486/gif.latex)

The rate of change of a function 
![[a, b]](https://cdn-s3.varsitytutors.com/uploads/formula_image/image/1085449/gif.latex)

Set 

The graph passes through the point 

and, substituting,
Solve for 

the correct response.
All HiSET: Math Resources


















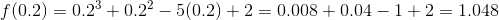





















































![[-2, -1.5]](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1085458/gif.latex)


















