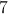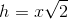Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Geometry

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #301 : Geometry

What is the area of a square that has a diagonal whose endpoints in the coordinate plane are located at (-8, 6) and (2, -4)?

Possible Answers:

50√2

200√2

100

100√2

Correct answer:

100

Explanation:

Square_part1

Square_part2

Square_part3

Report an Error

Example Question #21 : Triangles

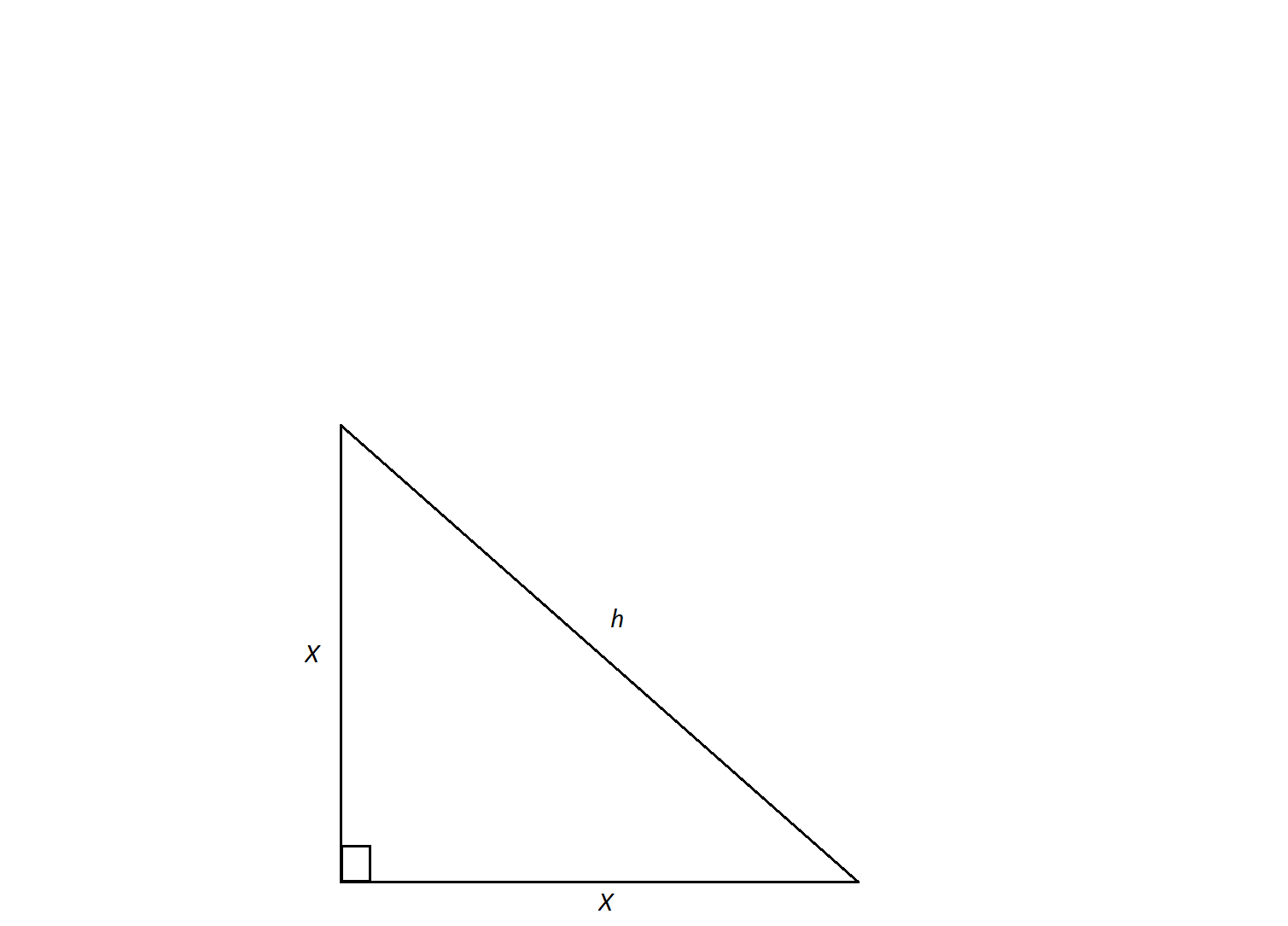
Isosceles

An isosceles triangle has a hypotenuse of h=7in . Find the length of its sides, .

Possible Answers:

Not enough information to solve

7in

5.94in

4.95in

2.64in

Correct answer:

4.95in

Explanation:

An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as $45^{\circ}-45^{\circ}-90^{\circ}$ triangles and their side lengths follow a specific pattern that states you can calculate the length of the legs of an isoceles triangle by dividing the length of the hypotenuse by the square root of 2

$x=\frac{h}{\sqrt{2}}$

$x=\frac{7in}{\sqrt{2}}$

$\rightarrow 4.95in$

Report an Error

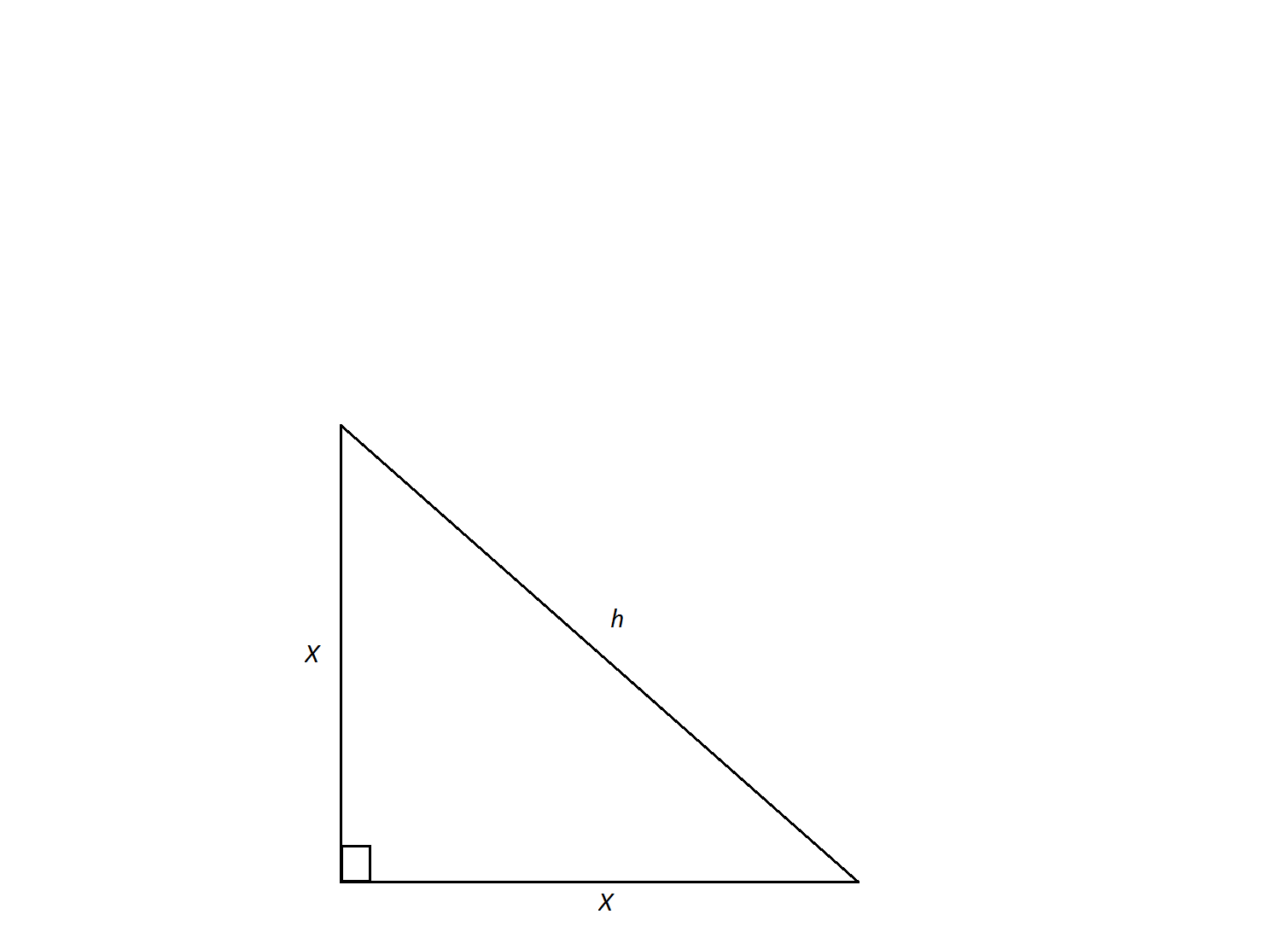
Example Question #1 : How To Find The Length Of The Side Of A 45/45/90 Right Isosceles Triangle

Isosceles

The measure of the sides of this isosceles right triangle are $x=3\sqrt{2}$ . Find the measure of its hypotenuse, .

Possible Answers:

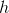
Not enough information to solve

Correct answer:

Explanation:

An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as $45^{\circ}-45^{\circ}-90^{\circ}$ triangles and their side lenghts follow a specific pattern that states you can calculate the length of the hypotenuse of an isoceles triangle by multiplying the length of one of the legs by the square root of 2.

$h=x\sqrt{2}$

$h=3\sqrt{2}*\sqrt{2}$

h=3*2

$\rightarrow6$

Report an Error

Example Question #1 : How To Find The Perimeter Of An Acute / Obtuse Triangle

Two similiar triangles have a ratio of perimeters of $7:2$ .

If the smaller triangle has sides of 3, 7, and 5, what is the perimeter of the larger triangle.

Possible Answers:

$50.5$

$52.5$

$48.5$

$49.5$

$51.5$

Correct answer:

$52.5$

Explanation:

Adding the sides gives a perimeter of 15 for the smaller triangle. Multipying by the given ratio of $\frac{7}{2}$ , yields 52.5.

Report an Error

Example Question #1 : How To Find The Perimeter Of An Acute / Obtuse Isosceles Triangle

Two sides of an isosceles triangle are 20 and 30. What is the difference of the largest and the smallest possible perimeters?

Possible Answers:

The answer cannot be determined

Correct answer:

Explanation:

The trick here is that we don't know which is the repeated side. Our possible triangles are therefore 20 + 20 + 30 = 70 or 30 + 30 + 20 = 80. The difference is therefore 80 – 70 or 10.

Report an Error

Example Question #2 : Acute / Obtuse Triangles

Two similiar triangles exist where the ratio of perimeters is 4:5 for the smaller to the larger triangle. If the larger triangle has sides of 6, 7, and 12 inches, what is the perimeter, in inches, of the smaller triangle?

Possible Answers:

Correct answer:

Explanation:

The larger triangle has a perimeter of 25 inches. Therefore, using a 4:5 ratio, the smaller triangle's perimeter will be 20 inches.

Report an Error

Example Question #1 : Acute / Obtuse Triangles

If a = 7 and b = 4, which of the following could be the perimeter of the triangle?

Msp30320bea9chb26d18hh0000627i1e4ibba8c4f5

I. 11

II. 15

III. 25

Possible Answers:

II Only

II and III Only

I Only

I and II Only

I, II and III

Correct answer:

II Only

Explanation:

Consider the perimeter of a triangle:

P = a + b + c

Since we know a and b, we can find c.

In I:

11 = 7 + 4 + c

11 = 11 + c

c = 0

Note that if c = 0, the shape is no longer a trial. Thus, we can eliminate I.

In II:

15 = 7 + 4 + c

15 = 11 + c

c = 4.

This is plausible given that the other sides are 7 and 4.

In III:

25 = 7 + 4 + c

25 = 11 + c

c = 14.

It is not possible for one side of a triangle to be greater than the sum of both of the other sides, so eliminate III.

Thus we are left with only II.

Report an Error

Example Question #1 : How To Find An Angle In An Acute / Obtuse Triangle

Solve for . (Not drawn to scale).

Possible Answers:

57^o

22^o

53^o

81^o

Correct answer:

53^o

Explanation:

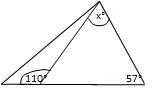
The angles of a triangle must add to 180^o. In the triangle to the right, we know one angle and can find another using supplementary angles.

57+(180-110)+x=180

Now we only need to solve for .

57+70+x=180

x=180-(57+70)=180-127

x=53^o

Report an Error

Example Question #1 : How To Find An Angle In An Acute / Obtuse Triangle

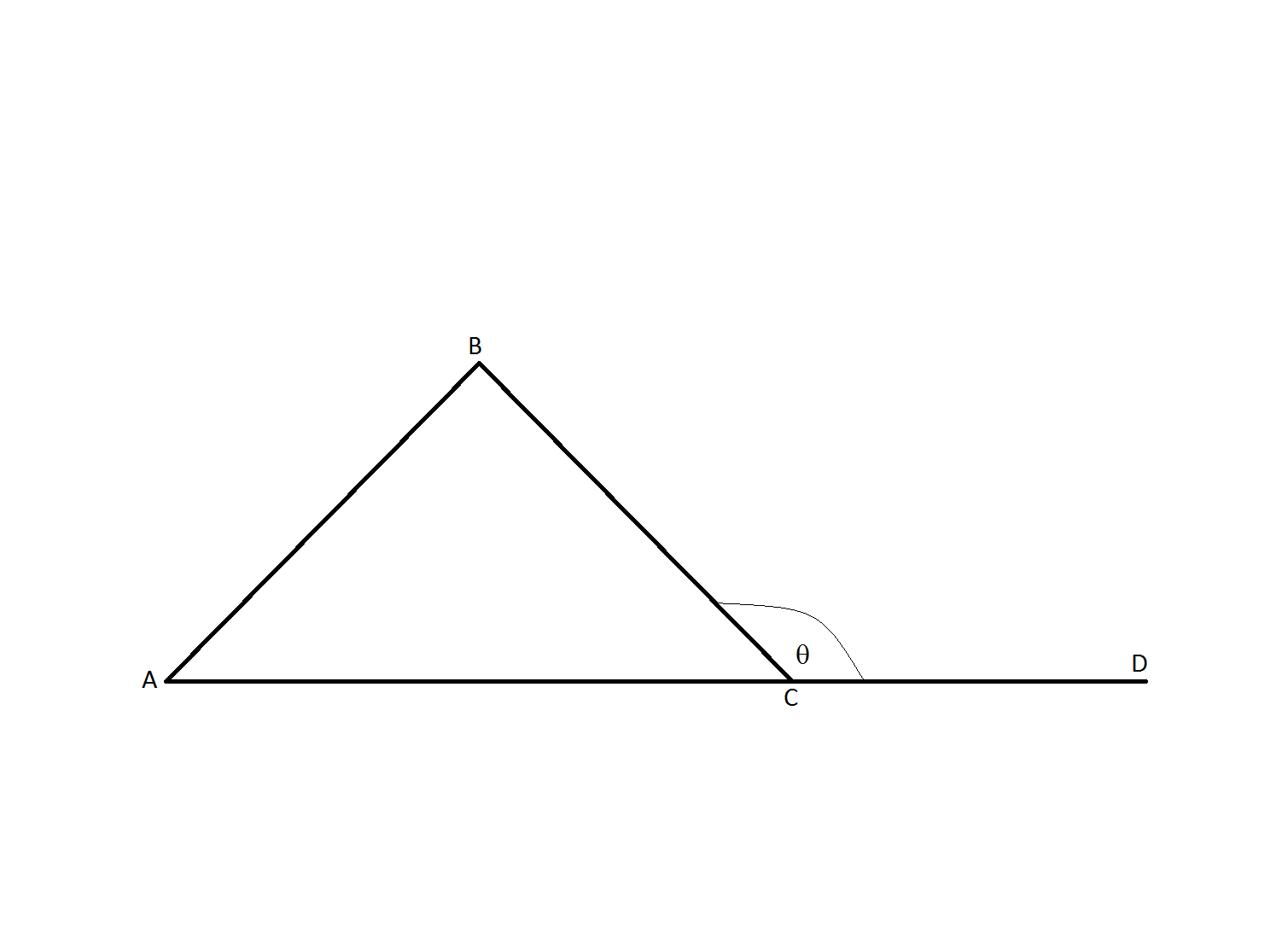Exterior_angle If $\angle A=42^{\circ}$ and $\angle B=76^{\circ}$ , what is the measure of $\theta$ ?

Possible Answers:

$62^{\circ}$

$76^{\circ}$

$118^{\circ}$

Not enough information to solve

$42^{\circ}$

Correct answer:

$118^{\circ}$

Explanation:

All of the interior angles of a triangle add up to $180^{\circ}$ .

If $\angle A=42^{\circ}$ and $\angle B=76^{\circ}$ , then

$\angle C= 180^{\circ}-(42^{\circ}+76^{\circ})$

Therefore, $\angle C=62^{\circ}$

Now, $\theta$ will equal $180^{\circ}-\angle C$ because $\angle C$ and $\theta$ form a straight line. Therefore,

$\theta=180^{\circ}-62^{\circ}$

$\rightarrow118^{\circ}$

Also, by definition, the angle of an exterior angle of a triangle is equal to the measure of the two interior angles opposite of it $\dpi{100} (\theta =76^{\circ}+42^{\circ}\rightarrow 118^{\circ})$ .

Report an Error

Example Question #1 : How To Find An Angle In An Acute / Obtuse Triangle

Two interior angles in an obtuse triangle measure $123^{\circ}$ and $11^{\circ}$ . What is the measurement of the third angle.

Possible Answers:

$50^{\circ}$

$46^{\circ}$

$104^{\circ}$

$57^{\circ}$

$123^{\circ}$

Correct answer:

$46^{\circ}$

Explanation:

Interior angles of a triangle always add up to 180 degrees.

Report an Error

View Tutors

Haazim
Certified Tutor

Howard University, Bachelor in Arts, English.

View Tutors

Alice
Certified Tutor

Bridgewater College, Bachelor in Arts, English. Longwood University, Certificate, Teacher Education, Multiple Levels.

View Tutors

Michele
Certified Tutor

University of Rome, Professional (JD, MD, DMD, etc), Law. Saint John's University -NY, Master of Science, Marketing.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SSAT Tutors in Boston, Physics Tutors in Seattle, English Tutors in Chicago, ISEE Tutors in Seattle, Biology Tutors in Washington DC, ACT Tutors in Los Angeles, SAT Tutors in Washington DC, Spanish Tutors in Atlanta, Spanish Tutors in San Francisco-Bay Area, MCAT Tutors in Philadelphia

Popular Courses & Classes

GRE Courses & Classes in Los Angeles, SSAT Courses & Classes in Atlanta, GMAT Courses & Classes in Miami, Spanish Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in Boston, SSAT Courses & Classes in Phoenix, ISEE Courses & Classes in Denver, GMAT Courses & Classes in Washington DC, MCAT Courses & Classes in Dallas Fort Worth

Popular Test Prep

MCAT Test Prep in Dallas Fort Worth, GRE Test Prep in Chicago, ACT Test Prep in San Diego, GRE Test Prep in Seattle, LSAT Test Prep in Denver, GRE Test Prep in San Francisco-Bay Area, MCAT Test Prep in San Francisco-Bay Area, ACT Test Prep in Dallas Fort Worth, MCAT Test Prep in Washington DC, SAT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Geometry

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #301 : Geometry

Example Question #21 : Triangles

Example Question #1 : How To Find The Length Of The Side Of A 45/45/90 Right Isosceles Triangle

Example Question #1 : How To Find The Perimeter Of An Acute / Obtuse Triangle

Example Question #1 : How To Find The Perimeter Of An Acute / Obtuse Isosceles Triangle

Example Question #2 : Acute / Obtuse Triangles

Example Question #1 : Acute / Obtuse Triangles

Example Question #1 : How To Find An Angle In An Acute / Obtuse Triangle

Example Question #1 : How To Find An Angle In An Acute / Obtuse Triangle

Example Question #1 : How To Find An Angle In An Acute / Obtuse Triangle

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: