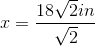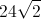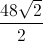All High School Math Resources
Example Questions
Example Question #171 : Triangles
A triangle has a perimeter of 


The answer is 
Since we know that the permieter is 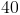


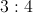





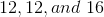

Example Question #20 : Isosceles Triangles
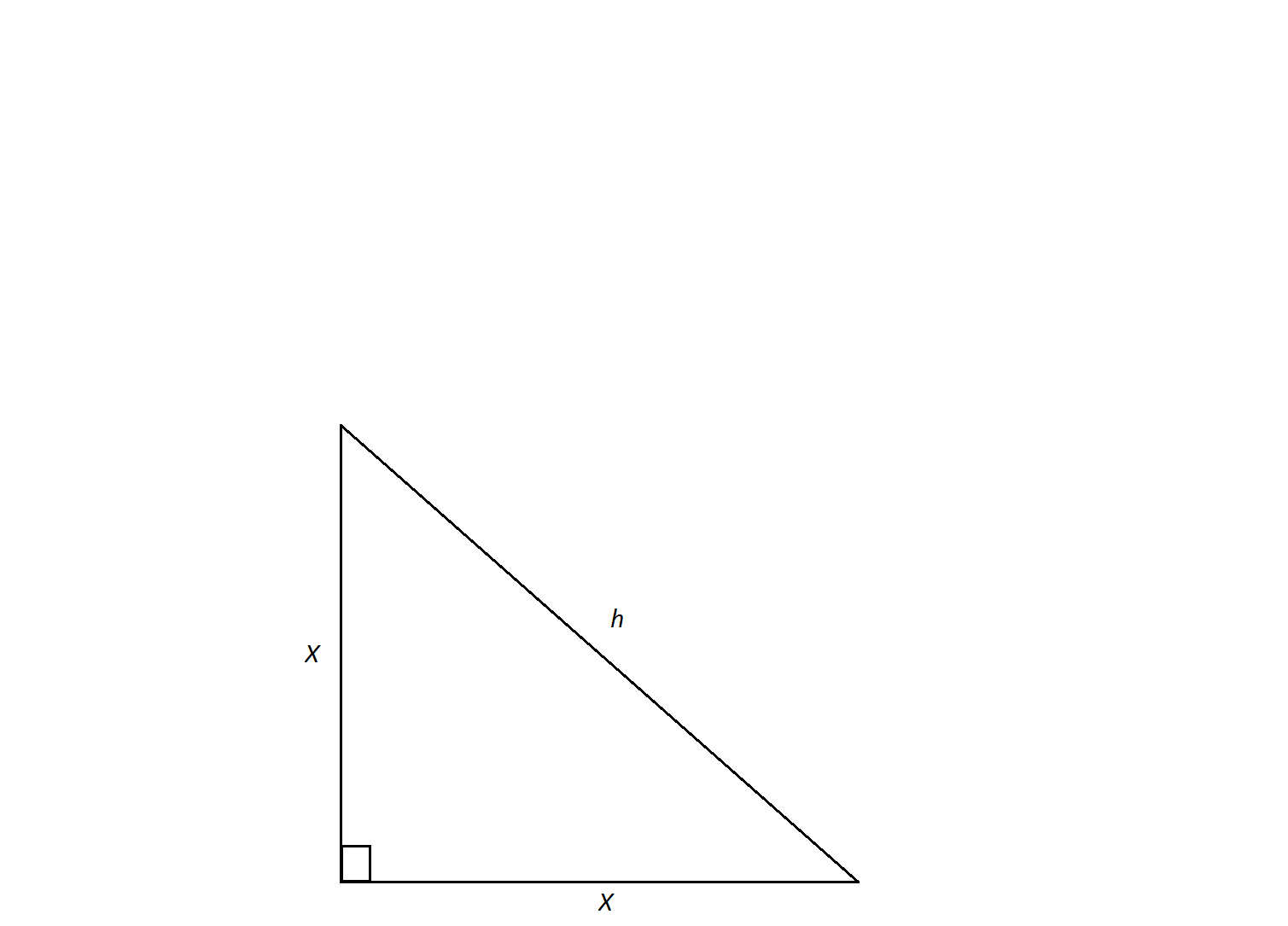
In an isosceles right triangle, two sides equal 

This problem represents the definition of the side lengths of an isosceles right triangle. By definition the sides equal 



Example Question #1 : 45/45/90 Right Isosceles Triangles
ABCD is a square whose side is 
none of the other answers
To find the length of the diagonal, given two sides of the square, we can create two equal triangles from the square. The diagonal line splits the right angles of the square in half, creating two triangles with the angles of 





Appyling this, if we plug 

Example Question #2 : 45/45/90 Right Isosceles Triangles
The area of a square is 
If the area of the square is 


Then, the diagonal creates two 

Example Question #1 : 45/45/90 Right Isosceles Triangles
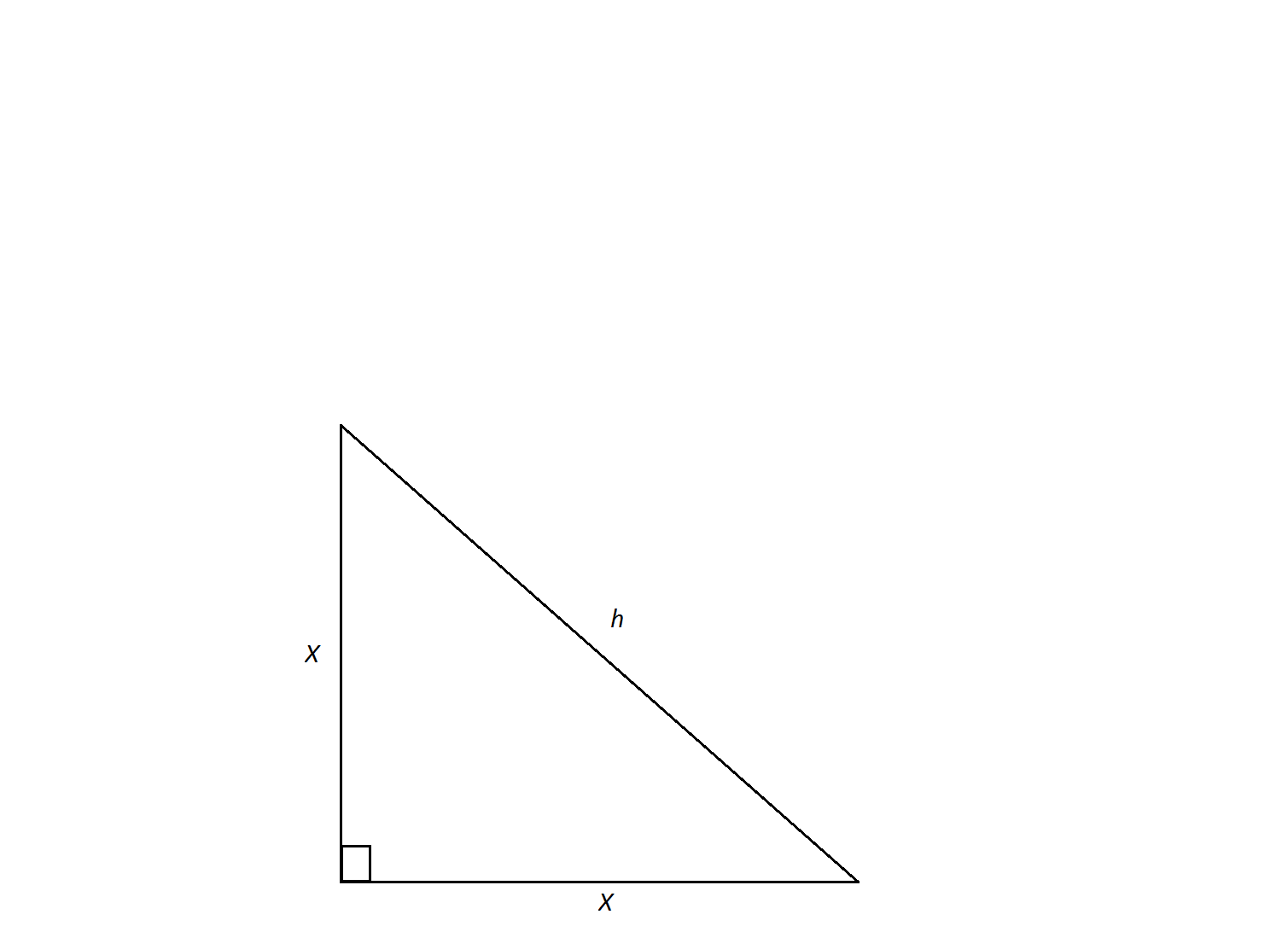
An isosceles right triangle has a hypotenuse of 
Not enough information to solve
In order to calculate the triangle's area, we need to find the lengths of its legs. An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as 
Now we can calculate the area using the formula
Now, convert to feet.
Example Question #2 : 45/45/90 Right Isosceles Triangles
The base of a right isosceles triangle is 8 inches. The hypotenuse is not the base. What is the area of the triangle in inches?
To find the area of a triangle, multiply the base by the height, then divide by 2. Since the short legs of an isosceles triangle are the same length, we need to know only one to know the other. Since, a short side serves as the base of the triangle, the other short side tells us the height.
Example Question #2 : 45/45/90 Right Isosceles Triangles
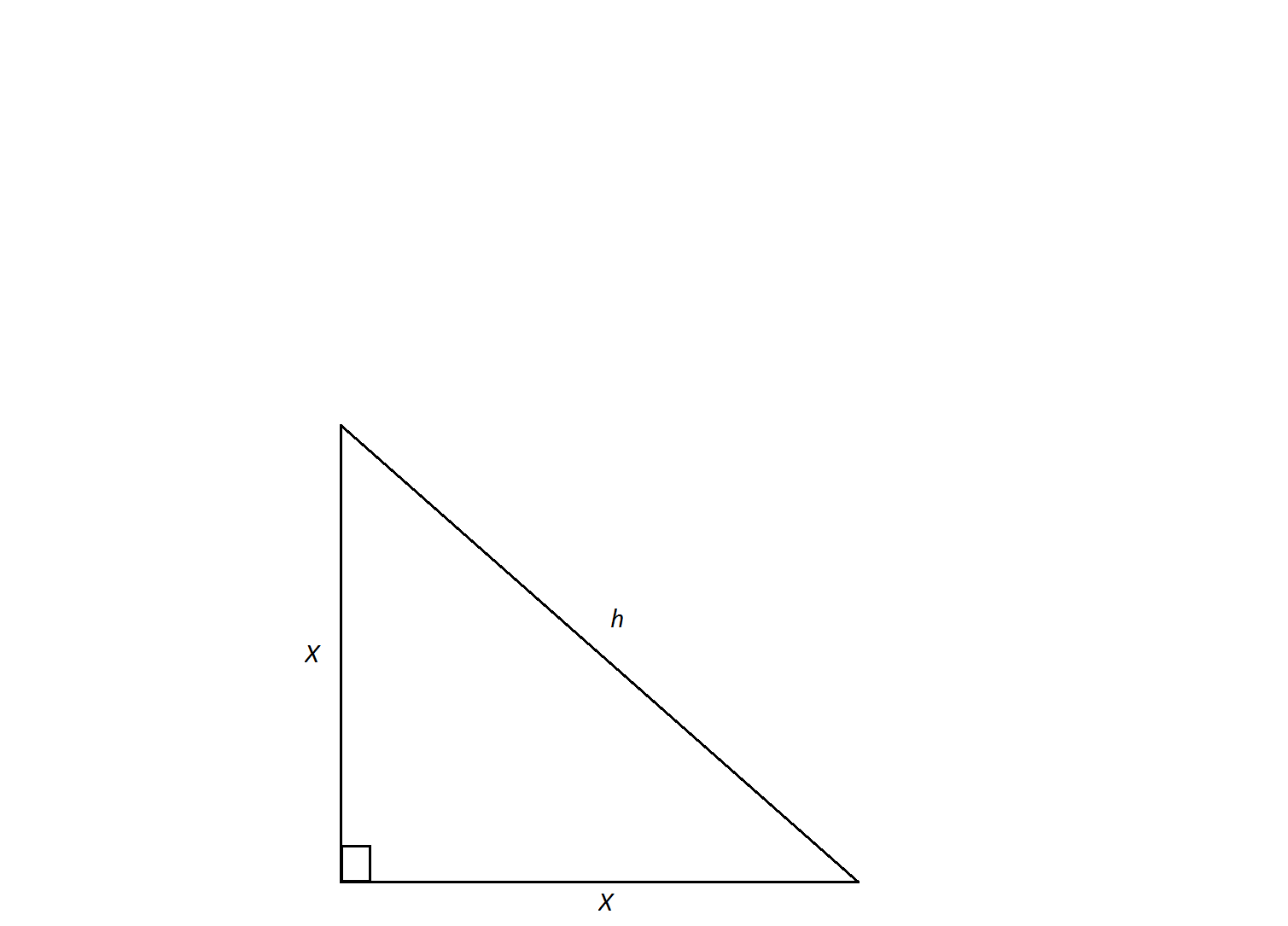
The hypotenuse of an isosceles right triangle has a measure of 
Not enough information to solve
In order to calculate the triangle's perimeter, we need to find the lengths of its legs. An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as 
Now we can calculate the perimeter by doubling 

Example Question #3 : 45/45/90 Right Isosceles Triangles

The side lengths of an isoceles right triangle measure 
Not enough information to solve
An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as 
Now we can calculate the perimeter by doubling 

Example Question #4 : 45/45/90 Right Isosceles Triangles
A triangle has two angles equal to 

When a triangle has two angles equal to 

The pattern for the sides of a 

Since two sides are equal to 

Add them all together to get 
Example Question #1 : How To Find The Perimeter Of A 45/45/90 Right Isosceles Triangle
An isosceles triangle has a base of 6 and a height of 4. What is the perimeter of the triangle?
None of these
An isosceles triangle is basically two right triangles stuck together. The isosceles triangle has a base of 6, which means that from the midpoint of the base to one of the angles, the length is 3. Now, you have a right triangle with a base of 3 and a height of 4. The hypotenuse of this right triangle, which is one of the two congruent sides of the isosceles triangle, is 5 units long (according to the Pythagorean Theorem).
The total perimeter will be the length of the base (6) plus the length of the hypotenuse of each right triangle (5).
5 + 5 + 6 = 16
Certified Tutor
All High School Math Resources