All High School Math Resources
Example Questions
Example Question #331 : Plane Geometry
What is the third angle in a triangle with angles of 


No such triangle can exist.



No such triangle can exist.
We know that the sum of the angles of a triangle must add up to 

Example Question #1 : Acute / Obtuse Triangles
Points A, B, C, D are collinear. The measure of ∠ DCE is 130° and of ∠ AEC is 80°. Find the measure of ∠ EAD.

80°
70°
50°
60°
50°
To solve this question, you need to remember that the sum of the angles in a triangle is 180°. You also need to remember supplementary angles. If you know what ∠ DCE is, you also know what ∠ ECA is. Hence you know two angles of the triangle, 180°-80°-50°= 50°.
Example Question #331 : Plane Geometry
If the average (arithmetic mean) of two noncongruent angles of an isosceles triangle is 
Since the triangle is isosceles, we know that 2 of the angles (that sum up to 180) must be equal. The question states that the noncongruent angles average 55°, thus providing us with a system of two equations:
Solving for x and y by substitution, we get x = 70° and y = 40° (which average out to 55°).
70 + 70 + 40 equals 180 also checks out.
Since 70° is not an answer choice for us, we know that the 40° must be one of the angles.
Example Question #171 : Geometry
Points A, B, and C are collinear (they lie along the same line). The measure of angle CAD is 


Find the measure of 
The measure of 








Because the measures of the three angles in a triangle must add up to 





Example Question #61 : Triangles
The base angle of an isosceles triangle is 
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Solve the equation 
x = 180 - 27 - 27
x = 126
Therefore the measure of the vertex angle is 
Example Question #11 : Isosceles Triangles
An isosceles triangle has an area of 12. If the ratio of the base to the height is 3:2, what is the length of the two equal sides?
5
3√3
6
4√3
4
5
Area of a triangle is ½ x base x height. Since base:height = 3:2, base = 1.5 height. Area = 12 = ½ x 1.5 height x height or 24/1.5 = height2. Height = 4. Base = 1.5 height = 6. Half the base and the height form the legs of a right triangle, with an equal leg of the isosceles triangle as the hypotenuse. This is a 3-4-5 right triangle.

Example Question #62 : Triangles
Two sides of a triangle each have length 6. All of the following could be the length of the third side EXCEPT
This question is about the Triangle Inequality, which states that in a triangle with two sides A and B, the third side must be greater than the absolute value of the difference between A and B and smaller than the sum of A and B.
Applying the Triangle Inequality to this problem, we see that the third side must be greater than the absolute value of the difference between the other two sides, which is |6-6|=0, and smaller than the sum of the two other sides, which is 6+6=12. The only answer choice that does not satisfy this range of possible values is 12 since the third side must be LESS than 12.
Example Question #1 : How To Find The Area Of An Acute / Obtuse Triangle
Find the area of a triangle whose base is 

This problem is solved using the geometric formula for the area of a triangle.
Convert feet to inches.
Example Question #333 : Plane Geometry
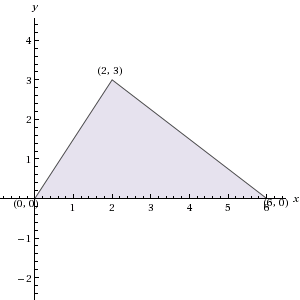
If triangle ABC has vertices (0, 0), (6, 0), and (2, 3) in the xy-plane, what is the area of ABC?
10
12
20
18
9
Example Question #1 : How To Find The Area Of An Acute / Obtuse Triangle
What is the area of a triangle with a height of 

When searching for the area of a triangle we are looking for the amount of the space enclosed by the triangle.
The equation for area of a triangle is
Plug the values for base and height into the equation yielding
Then multiply the numbers together to arrive at the answer 
Certified Tutor
All High School Math Resources